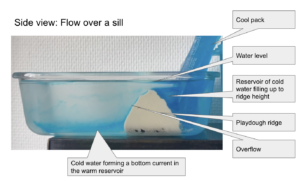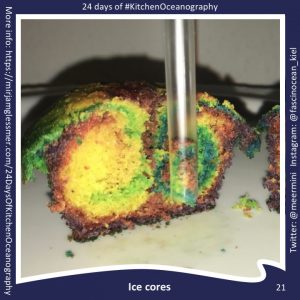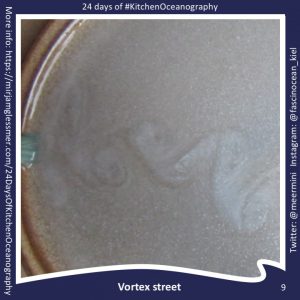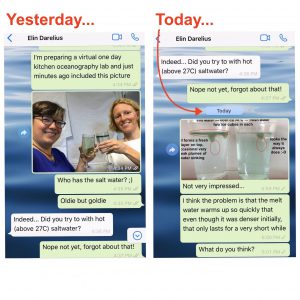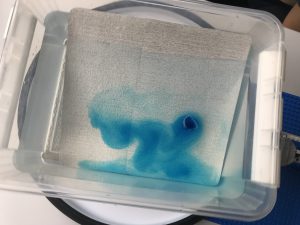demonstration (easy) Archives - Adventures in Oceanography and Teaching

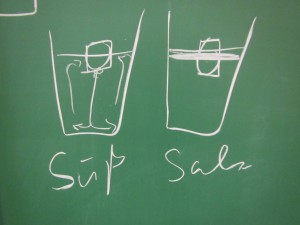
Throwback to the pandemic and teaching from home: “An ocean in a bucket”

May 1, 2025

I had completely forgotten about a video that Kjersti and I produced in 2021 to prepare her students for rotating tank experiments by addressing a common misconception before they ever…

New SERC “Teach the Earth” Activity on “Ocean Currents and Overflows”

May 23, 2024

One day in the office at the Geophysical Institute in Bergen last Friday, and for the first time in a long time I am writing a little bit of oceanography…

24 days of #KitchenOceanography — now available as a book!

August 28, 2023

24DaysOfKitchenOceanography

For all of you who know and love my “24 days of #KitchenOceanography” series (and for those who need to quickly look up what that was about and then fall…

A simple way to visualize how hydrostatic pressure increases with depth

February 25, 2023

I did this demo for my freediving club Active Divers (and if you aren’t following us on Insta yet, that’s what I am taking all these pretty pictures for!): 1.5l PET…

Denmark Strait overflow in a tank experiment

February 24, 2023

Since our Denmark Strait tank experiment from 2013 (see here in a post from 2014!) is still the one I refer to when I want to point to pictures of…

Using coffee in a talk on kitchen oceanography

October 21, 2021

I have been a bit quiet on here recently, because I had so many exciting projects going on that I did not manage to document them in real time (well,…

Molecular diffusion at different temperatures (involving tea bags and some convection)

August 30, 2021

I thought I had posted the picture below some time in winter already, but when I recently searched for it, I couldn’t find it. So either I didn’t post it,…

Coffee in #KitchenOceanography

February 16, 2021

For some reason my workflow regarding all things #KitchenOceanography and #WaveWatching changed at the beginning of this year. I started editing frames on the pictures I’m posting on Instagram, and,…

About #KitchenOceanography

February 15, 2021

At the end of last year, I did a poll on Twitter, asking what people would like to see more of in 2021: Kitchen oceanography, wave watching, teaching & scicomm…

24 Days of #KitchenOceanography — Sea level rise

December 24, 2020

24 Days of #KitchenOceanography — Melting ice cubes that are forced to the bottom of a beaker

December 23, 2020

24 Days of #KitchenOceanography — Sea level rise

December 22, 2020

24 Days of #KitchenOceanography — Ice cores

December 21, 2020

24 Days of #KitchenOceanography — Resublimation

December 20, 2020

24 Days of #KitchenOceanography — Crystal structure of ice

December 19, 2020

My iEarth “Christmas Lecture” on #KitchenOceanography

December 19, 2020

I gave a talk withing iEarth’s seminar series to introduce myself to the network last week. And since it was the last lecture before the Christmas break, I tried to turn it…

24 Days of #KitchenOceanography — Fresh water and salt water ice crystal structure

December 18, 2020

24 Days of #KitchenOceanography — Diffusive layering

December 17, 2020

24 Days of #KitchenOceanography — Double-diffusive mixing with cream and tea

December 16, 2020

24 Days of #KitchenOceanography — Double-diffusive mixing

December 15, 2020

24 Days of #KitchenOceanography — Topographic mixing

December 14, 2020

24 Days of #KitchenOceanography — Wind-driven mixing

December 13, 2020

24 Days of #KitchenOceanography — Transport of substances

December 12, 2020

24 Days of #KitchenOceanography — Eddy in a jar

December 11, 2020

24 Days of #KitchenOceanography — Mediterranean Outflow

December 10, 2020

24 Days of #KitchenOceanography — Vortex street

December 9, 2020

24 Days of #KitchenOceanography — Visualizing streamlines

December 8, 2020

24 Days of #KitchenOceanography — Hydraulic jump in the sink

December 7, 2020

24 Days of #KitchenOceanography — Surface waves and internal waves

December 6, 2020

24 Days of #KitchenOceanography — Overflow experiment

December 5, 2020

24 Days of #KitchenOceanography — Melting ice cubes!

December 4, 2020

24 Days of #KitchenOceanography — Density-driven currents

December 3, 2020

24 Days of #KitchenOceanography — Oceanic overturning circulation

December 2, 2020

24 Days of #KitchenOceanography — Layers in the ocean

December 1, 2020

Rotating vs non-rotating turbulence

June 9, 2020

Last Thursday, Torge & I invited his “atmosphere & ocean dynamics class” to a virtual excursion into my kitchen — to do some cool experiments. As you know, I have…

Thermal forcing vs rotation tank experiments in more detail than you ever wanted to know

May 25, 2020

This is the long version of the two full “low latitude, laminar, tropical Hadley circulation” and “baroclinic instability, eddying, extra-tropical circulation” experiments. A much shorter version (that also includes the…

Thermal forcing vs rotation

May 23, 2020

The first experiment we ever ran with our DIYnamics rotating tank was using a cold beer bottle in the center of a rotating tank full or lukewarm water. This experiment is…

Ekman layers in my kitchen

May 21, 2020

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough…

Rossby-#WaveWatchingWednesday

May 20, 2020

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough…

Brine rejection and overturning, but not the way you think! Guest post by Robert Dellinger

April 16, 2020

It’s #KitchenOceanography season! For example in Prof. Tessa M Hill‘s class at UC Davis. Last week, her student Robert Dellinger posted a video of an overturning circulation on Twitter that got me…

On melting ice cubes and molecular diffusion of heat

April 7, 2020

First of all, let me say how much I love having chats like the one Elin and I had over the weekend (which you only see the very beginning of…

Temperature dependency of molecular diffusion, and convection taking over

April 6, 2020

I saw the idea for this experiment on Instagram (Max is presenting it for @glaeserneslabor) and had to try it, too! The idea is to put drops of dye into…

Reposting my “field report” for the DIYnamics blog

March 13, 2020

DIYnamics

Reposting a guest post I wrote for the @DIYnamicsTeam‘s blog: When we came across the DIYnamics article right after its publication, Torge and I (Mirjam) were very excited about the…

A recent seminar presentation on “one should really play more!” and our rotating tanks

January 24, 2020

DryTheory2JucyReality

Using “One should really play more!” as title of a presentation in a serious scientific colloquium might seem like a bold move, but the gamble payed off: a large, interested…

Playing for #FlumeFriday

January 17, 2020

DryTheory2JucyReality

Yesterday, we’ve had four rotating tables operating simultaneously, for three different experiments. The one that everybody is gathering around in the picture above is our favourite experiment: a slowly rotating…

Thermal forcing in a non-rotating vs rotating case: Totally different results

November 23, 2019

On Thursday, I wrote about the thermally driven overturning circulation experiment that Torge and I did as past of our “dry theory 2 juicy reality” experiments, and mentioned that it…

Salt fingers in my overturning experiment

November 22, 2019

You might have noticed them in yesterday’s thermally driven overturning video: salt fingers! In the image below you see them developing in the far left: Little red dye plumes moving…

Thermally driven overturning circulation

November 21, 2019

Today was the second day of tank experiments in Torge’s and my “dry theory 2 juicy reality” teaching innovation project. While that project is mainly about bringing rotating tanks into…

If one rotating table is awesome, four rotating tables are…?

October 24, 2019

I’m actually at a loss for words. Amazing? Spectacular? So much fun? All of that! Today was the first time Torge and I tried our four DIYnamics-inspired rotating tables in…

Phase and group velocities in deep and shallow water

October 14, 2019

When Tor came to visit me in GFI’s basement lab a couple of days ago, he told me about an experiment he had seen in Gothenburg in the seventies. So…

Planetary Rossby waves on Beta-plane. A super easy tank experiment!

September 13, 2019

This is seriously one of the easiest tank experiments I have ever run! And I have been completely overthinking it for the last couple of weeks. Quick reminder: This is…

Tidal mixing on a (fjord’s) sill

August 12, 2019

A pink swirl going across a styrofoam block underneath a layer of yellow water? What’s going on here? The picture was taken in a water tank, simulating the circulation of…

Melting ice cubes experiment published in kids’ journal Frontiers Young Minds

June 28, 2019

Frontiers for Young Minds

On publishing in a journal peer-reviewed by kids, and suggesting it as a first journal new PhD students should be asked to write for You guys might remember my favourite…

My kids’ article on the formation of sea ice is out!

June 15, 2019

I recently published an article about how sea ice forms which, I think, turned out pretty well. But the coolest thing is the illustration that Jessie Miller did to go along with…

Ostfriesentee — Double diffusion in a tea cup

April 26, 2019

Showing double-diffusive mixing in tank experiments is a pain if you try to do it the proper way with carefully measured temperatures and salinities. It is, however, super simple, if…

#kitchenoceanography or #bathtubphysics? Playing with cool phenomena, water and dye

March 31, 2019

Some bathtub magic today! Let’s take a paper kitchen towel and an empty glass. Squish the paper towel into the empty glass, submerge it upside down into the water aaand……

A little get-better-soon physics

March 14, 2019

…because nothing cheers me up like playing with water ;)

#KitchenOceanography with Judith and her hot chocolate

January 25, 2019

Let’s talk about zonal jets! They keep popping into my life all the time right now, and that has got to mean something, right? Zonal jets, for all that are…

Guest post: Alice shows magic tricks and explains refraction of light in water

January 12, 2019

My friend Alice Langhans runs a super cool science communication Instagram (@edu_al_ice), where she posts about her experiences as PhD student in physics education research. And there is a lot more…

Bottom Ekman layer without a rotating table

October 31, 2018

Can you do a bottom Ekman layer demonstration without a rotating table? That’s the kind of challenge I like :-) The way I’ve previously showed bottom Ekman layers is by…

Update on freezing ice cubes and the temperature distribution in our freezer

October 10, 2018

After writing the blog post on sea ice formation, brine release and what ice cubes can tell you about your freezer earlier today, I prepared some more ice cubes (because you…

Sea ice formation, brine release, or: What ice cubes can tell you about your freezer

October 10, 2018

Many of my kitchen oceanography experiments use dyed ice cubes, usually because it makes it easier to track the melt water (for example when looking at how quickly ice cubes…

Thinking about the Doppler effect as of a boat sailing against the waves!

September 25, 2018

I can’t believe I haven’t written about this on my blog before, thanks Markus Pössel for reminding me of this great way to understand the Doppler effect! Doppler effect, or…

Experiment: Double-diffusive mixing (salt fingering)

August 24, 2018

On the coolest process in oceanography. My favorite oceanographic process, as all of my students and many of my acquaintances know, is double-diffusive mixing. Look at how awesome it is:…

Experiment: Temperature-driven circulation

August 20, 2018

My favorite experiment. Quick and easy and very impressive way to illustrate the influence of temperature on water densities. This experiment is great if you want to talk about temperature…

Tides themselves don’t induce (a lot of) mixing, only tides hitting topography do. An experiment.

August 17, 2018

As you might have noticed, the last couple of days I have been super excited to play with the large tanks at GFI in Bergen. But then there are also…

Experiment: Oceanic overturning circulation (the slightly more complicated version)

August 15, 2018

The experiment presented on this page is called the “slightly more complicated version” because it builds on the experiment “oceanic overturning circulation (the easiest version)” here. Background One of the…

Experiment: Oceanic overturning circulation (the easiest version)

August 10, 2018

“The easiest” in the title of this page is to show the contrast to a “slightly more complicated” version here. Background One of the first concepts people hear about in the context…

Experiment: Eddy in a jar

August 6, 2018

Rotating experiments in your kitchen. Eddies, those large, rotating structures in the ocean, are pretty hard to imagine. Of course, you can see them on many different scales, so you…

Experiment: Demystifying the Coriolis force

August 3, 2018

Mirjam S. Glessmer & Pierré D. de Wet Abstract Even though experiments – whether demonstrated to, or personally performed by students – have been part of training in STEM for…

Experiment: Influence of stratification on mixing

August 1, 2018

A wind stress is applied to the surface of a stratified and a non-stratified tank to cause mixing. This is a pretty impressive experiment to run if you have a…

Experiment: Interference of waves

July 27, 2018

interference

Interference of waves is something often taught either using light as a practical example, or without a practical example. Here I want to show a couple of observations as well…

Experiment: Ice cubes melting in fresh water and salt water

July 23, 2018

Explore how melting of ice cubes floating in water is influenced by the salinity of the water. Important oceanographic concepts like density and density driven currents are visualized and can…

Cloud in a bottle experiment

March 4, 2018

Guest post by Susann Tegtmeier (written two months ago, I just never got around to posting it. Sorry!) — No one likes clouds when they bring rain, but what if…

The energy lab’s dry run. Or: I have a great team! :-)

December 15, 2017

At first, I wanted to call this blog post “behind the scenes of a school lab” until I looked through the pictures and realized that all I am showing is…

My new school lab on energy in the climate system has been launched! :-)

December 15, 2017

Today was a very exciting day: We launched my new school lab on energy in the climate system! The “energie:labor” is finally up and running again! Let me walk you…

Of cupcakes and ice cores

December 2, 2017

For a popular science presentation on climate change, I needed a simple illustration for how ice cores can be used as archives of past climates. Luckily, my sister and family…

Observing the “melting ice cubes” experiment with a thermal imaging camera

November 18, 2017

Remember the melting ice cube experiment? Great! If I had the chance to teach an intro to oceanography or some other class where I have time with students over a…

Melting ice cubes & thermal imaging camera

June 12, 2017

I haven’t talked about my favourite experiment in a long time (before using it last week in the MeerKlima congress and suddenly talking about it all the time again), because I…

My workshop at MeerKlima.de

June 8, 2017

Today I ran a workshop at the MeerKlima.de congress in Hamburg: A congress for high school students, organised by a student committee. The large lecture theatre of the chemistry department at…

Workshop prep and a riddle

June 7, 2017

Looking at the picture below, can you guess which experiment I am going to do at the MeerKlima.de workshop? Yep, my favourite experiment — melting ice cubes! :-) And I am…

Pythagoras’ Cup

February 28, 2017

Yep, I’ve been playing this weekend :-) After seeing this on Facebook a while back I just couldn’t resist… Enjoy! :-)

Newton’s balls

February 16, 2017

Phaenomenta Flensburg

Those are always fun! :-) Again seen at Phaenomenta Flensburg.

Fictitious forces (2/5): Experiencing frames of reference on a playground

January 19, 2017

How can you be moving in one frame of reference, yet not moving in another? We talked about the difficulty of different frames of reference recently, so today I want…

Fictitious forces (1/5): Record players and Coriolis deflection

January 17, 2017

An experiment showing how seemingly straight trajectories can be transformed into curly ones. One of the phenomena that are really not intuitive to understand are fictitious forces. Especially relevant in…

Evaporating sea water

January 3, 2017

How much salt is there in sea water? What concentration do you need before crystals start forming? What will those crystals look like? I am sure those are the kind…

Taking the hydrostatic paradox to the next (water) level

April 14, 2016

How well do people understand hydrostatics? I am preparing a workshop for tomorrow night and I am getting very bored by the questions that I have been using to introduce…

Ice cubes melting in fresh water and salt water. By Mirjam S. Glessmer

Using the “melting ice cube” experiment to let future instructors experience inquiry-based learning.

April 5, 2016

Using the “melting ice cube” experiment to let future instructors experience inquiry-based learning. I recently (well, last year, but you know…) got the chance to fill in for a colleague…

Making a spinningtop from a metal paper clip

February 2, 2016

spinningtop

One of my favourite memories of my physics classes at university is of the day when the professor brought in metal paper clips for everybody — to make spinning tops!…

Spinningtop trajectories

January 14, 2016

spinningtop

A new physics toy in my house: A spinning top that has a pen as its tip and leaves trajectories as it spins! The trajectories are really cool. Depending on…

Water seeks its level. U-tube experiment. By Mirjam S. Glessmer

When water doesn’t seek its level

January 12, 2016

Last week we talked about misconceptions related to hydrostatic pressure, and how water always seeks its level. Today I’m gonna show you circumstances in which this is actually not the…

Water seeks its level

January 7, 2016

There are a lot of misconceptions related to hydrostatic pressure. One of them is that if you took a jug like the one below (or a U-tube, as in my…

My favorite demonstration of the coolest mixing process: Salt fingering!

December 15, 2015

I am updating many of my old posts on experiments and combining multiple posts on the same topic to come up with a state-of-the-art post, so you can always find the…

Why does the sun have to be a lot further from us than the moon? A deduction.

November 9, 2015

Remember the hands-on demo of the phase of the moon? Holding a sphere up in the sunlight in the direction of the moon, the sphere will show the same phase…

Temperature-driven overturning experiment – the easy way

November 6, 2015

In my last post, I showed you the legendary overturning experiment. And guess what occurred to me? That there is an even easier way to show the same thing. No gel…

Overturning experiment. By Mirjam S. Glessmer

A very simple overturning experiment for outreach and teaching

November 4, 2015

For one of my side-projects I needed higher-resolution photos of the overturning experiment, so I had to redo it. Figured I’d share them with you, too. You know the experiment: gel…

Interference of waves

September 4, 2015

The advantage of wind-less days on a sailing holiday is that you can play with water as much as you like. For example in order to look at the interference…

On buoyancy

September 2, 2015

This is an experiment that Martin brought to Ratzeburg and that he let me use on my blog: Using a beam balance to talk about buoyancy. So at first we…

Sink or swim – experiments using tin foil

August 26, 2015

A pet peeve of mine are books on handcrafts or experiments or any kind of activity that come with drawings instead of pictures, because I always suspect that it was…

Creating eddies

August 24, 2015

I always love watching paddles in water, or ships in water, or ducks in water, or anything water, really, but on a wind-less day in Ratzeburg, Siska managed to create…

Playing with a model steam boat

August 21, 2015

RZ2015

I’ve shown this steam boat before, but I thought you might appreciate it in its full glory on the lake in Ratzeburg. Plus this time round, in the movie below,…

Stream lines and paper towels

July 15, 2015

We’ve been talking about stream lines a lot recently (see for example the flow around a paddle or flow around other stuff). I’ve always heard stories about a neat way of…

Water bottle & bike pump rocket

June 19, 2015

CVK

This is another one of the experiments from the aerodynamics experiments kit that I borrowed at work (see here). We’ve all seen water bottle & bike pump rockets before, but…

Ball balancing on air flow

June 15, 2015

Recently, someone at my university told me about a case of experiments connected to aerodynamics* that they occasionally use for demonstrations and outreach. Obviously, I asked if I might possibly…

When diet coke cans don’t float better than regular coke cans

April 17, 2015

This is why you should always test an experiment before you run it… On recent travels, when I saw that they were serving drinks out of tiny cans, I asked…

Vortex streets on a plate

February 23, 2015

You might think that three hours of canoe polo on a Saturday morning would be enough water for the day, but no. As when I did the experiment for the “eddies in a…

Signal velocity

February 18, 2015

How can a signal travel faster than the phase of a wave, or individual particles? I remember having a really hard time with the concept of a signal traveling faster…

Eddies in a jar

January 28, 2015

Rotating experiments in your kitchen. Do you know those Saturday mornings when you wake up and just know that you have to do oceanography experiments? I had one of those…

Playing with time lapse

January 26, 2015

One of my not-so-bright ideas as you’ll see… Last week we talked about the thought experiment on how all objects have to fall at the same rate. Which is clearly only…

Heat engine – drinking bird

January 19, 2015

A heat engine. This is my sister’s drinking bird (which I was asked to mention explicitly). If you don’t know how they work, check out the image below or the…

Steam boat

January 16, 2015

A pop pop boat in action! Following up on the steam-powered spinning top we talked about earlier, today we have a steam-powered pop pop boat. The mechanism is exactly the…

Steam-powered spinning top

January 12, 2015

How changing the state of water can drive motion. Somehow over the holidays we ended up playing with a lot of toys related to the change of state of water,…

Which displaces more water, a boat with the anchor onboard or in the water?

December 5, 2014

Not that this is a big effect in the ocean, but still, it’s a nice demo. A body submerges into the water until it displaces an amount of water that is…

Building a miniature well

November 28, 2014

hands-on activity

Groundwater dynamics in the kitchen. This activity is suitable for young children who wonder where the tap water comes from. All you need is some sand, an empty toilet paper roll, and…

Fog and clouds in a bottle

November 21, 2014

A little bit of hands-on meteorology for a change. This post is inspired by www.planet-science.com‘s “fog in a bottle” and “make a cloud in a bottle” posts. Inspired meaning that…

Tides in a glass

October 31, 2014

A very simple experiment to show how waves can travel around an ocean basin. I wrote these instructions for a book project that I was lucky enough to get involved…

Ice cubes melting at the bottom of the beakers

October 13, 2014

Because surely there is one more post in this topic? ;-) For those of you who haven’t heard about the “melting ice cube” obsession of mine, please check out the…

Why folic acid might be good for people, but not so good for tank experiments

October 6, 2014

I had to do the complete series of experiments, of course… The other day I mentioned that I had used salt from my kitchen for the “ice cubes melting in…

Melting ice cubes, again

October 3, 2014

Somehow I am stuck on this demonstration! I can’t let go of this experiment. Last time I posted about it, someone (Hallo Papa!) complained about the background and how I…

Conducting experiments at EMSEA14

October 1, 2014

Kristin’s and my workshop at EMSEA14. As I mentioned before, Kristin Richter and I are running the workshop “Conducting oceanographic experiments in a conventional classroom anywhere” at the European Marine Science…

The icy elevator

September 29, 2014

Weird things happening when ice cubes melt. Remember I said that there were weird and wonderful things going on when I last ran the melting ice cubes in salt and…

Melting ice cubes reloaded

September 26, 2014

Or why you should pay attention to the kind of salt you use for your experiments. The melting ice cubes in salt and fresh water is one of my favorites that…

Learning with fluid toys

September 22, 2014

How fluid toys can be used to demonstrate principles of fluid mechanics. I guess every attempt to hide that I LOOOOVE fluid toys of any kind is futile. So imagine…

Thermally driven circulation

August 28, 2014

One of my all-time favorite experiments. The salt group got a bit bored from watching ice cubes melt, so I suggested they look at temperature differences for a change, and…

Wave interference in a tank

August 25, 2014

Creating waves and watching them interfere. (deutscher Text unten) You might not have guessed it from reading about our waves meeting over a sandbank experiment, but we weren’t doing in…

Thermally-driven overturning circulation

August 23, 2014

Cooling on one end of the tank, heating on the other: A temperature-driven overturning. [deutscher Text unten] Always one of my favorite experiments – the overturning experiment (and more, and more).…

Surface tension with a twist

August 11, 2014

The coolest surface tension demonstration yet! Just because it is AWESOME. Enjoy! Watch the video here. oh, you didn’t think I would only post one video, did you? ;-)

Capillary effects

July 4, 2014

When hydrostatics just doesn’t explain things. Occasionally one notices water levels in straws that are slightly above the water levels in the glass. And of course – even though we…

Marsigli’s experiment

June 4, 2014

Density-driven flow. The experiment presented in this post was first proposed by Marsigli in 1681. It illustrates how, despite the absence of a difference in the surface height of two fluids,…

Surface tension and office supplies.

May 21, 2014

Lots of stuff an be made to float on water just because of surface tension. This morning, I was taking pictures of heaps of waters on coins. I was planning to…

Surface tension – heaps of water.

May 19, 2014

The classical way of demonstrating surface tension. When talking about surface tension, the classical thing to do is to talk about the shape of drops of water. As seen before…

Refraction of light in water – coins and lenses.

May 9, 2014

More on what water can do to light. Remember my fascination with dandelions? Just to remind you: Especially in combination with coins and water droplets, dandelions are a source of…

Guest post: The mystery of the cold room

April 30, 2014

Guest post by Kristin Richter! Today I’m excited to bring to you a guest post from Innsbruck, Austria, written by my friend Kristin Richter. Kristin ran the oceanography lab in Bergen…

Vacuum pumps

April 20, 2014

What else did you think we tested them on? Before using my parents’ vacuum pumps (“vacuum” being used in a loose sense of the word…) on water in this post, we…

Bubble size depending on pressure

April 16, 2014

More playing with a vacuum pump. In this post, we talked about how decreasing the pressure on water can make dissolved gases come out of solution. But what happens if…

Gases dissolved in water

April 14, 2014

A simple experiment to show that there are really gases dissolved in water. Luckily, my parents like to play at least as much as I do. So when I got…

Lava

April 10, 2014

Don’t you just love lava lamps? I got a lot of weird looks when I excitedly told people about two years ago that I had just bought a lava lamp.…

An overturning experiment (part 3)

March 7, 2014

By popular demand: A step-by-step description of the overturning experiment discussed here and here. I wrote this description a while ago and can’t be bothered to transfer it into the…

An overturning experiment (part 2)

March 5, 2014

How to adapt the same experiment to different levels of prior knowledge. In this post, I presented an experiment that I have run in a primary school, with high-school pupils,…

An overturning experiment

March 3, 2014

A simple experiment that shows how the large-scale thermally-driven ocean circulation works. Someone recently asked me whether I had ideas for experiments for her course in ocean sciences for non-majors.…

Modeling the Denmark Strait Overflow

February 24, 2014

Ha, this is a bad pun. We are modeling the Denmark Strait Overflow – but in a non-numerical, small-scale-and-playdough kind of way. More than a year ago, Kjetil and I ran…

Non-leaking bottle.

February 7, 2014

Still more on hydrostatic pressure. Just because it is cool :-)

Barometer problem.

January 31, 2014

Still talking about hydrostatic pressure. Yes, I am not done with hydrostatic pressure yet! One of the problems students were given in the study “Identifying and addressing student difficulties with…

Cartesian diver – organic version

January 22, 2014

Using orange peel as cartesian divers. Guess what my mom told me when we were playing with cartesian divers the other day? That orange peel works really well as a…

Cartesian diver

January 20, 2014

Compressibility of water and air. Today I want to talk about the different compressibilities of water and air. Actually, no, I just want to show you an experiment. One way…

Non-newtonian fluids.

January 17, 2014

kitchen oceanography

Playing with cornstarch and water. The other day my mom and I played with cornstarch and water. I have always been wanting to experiment more with non-newtonian fluids, and then…

Molecular diffusion of heat and salt

January 15, 2014

Why heat and salt diffuse at different rates. Why do heat and salt diffuse at different rates? This seems to always be puzzling students when talking about double diffusion. Well,…

Salt fingering – DIY

January 13, 2014

How to easily set up the stratification for the salt fingering process. Setting up stratifications in tanks is a pain. Of course there are sophisticated methods, but when you want…

Diffusive layering. Or: This is not a trick question!

January 10, 2014

The “other” double-diffusive mixing process. After having talked extensively about double diffusive mixing in my courses, I tend to assume that students not only remember that there is such thing as…

Salt fingering

January 8, 2014

How to show my favorite oceanographic process in class, and why. As I mentioned in this post, I have used double-diffusive mixing extensively in my teaching. For several reasons: Firstly,…

Double-diffusive mixing

January 6, 2014

On the coolest process in oceanography. My favorite oceanographic process, as all of my students and many of my acquaintances know, is double-diffusive mixing. Look at how awesome it is:…

Mediterranean outflow

December 2, 2013

Students demonstrating the mediterranean outflow in a tank. As reported earlier, students had to conduct experiments and present their results as part of CMM31. Niklas chose to demonstrate the mediterranean outflow…

The broken spoon

November 6, 2013

Refraction of light in water. I just happened to notice this the other day, so I thought I’d take a picture and share it with you. It is amazing how…

Water seeks its level.

November 4, 2013

A solution for the siphon problem of the fjord circulation experiment. After having run the fjord circulation experiments for several years in a row with several groups of students each…

Why do we get an Ekman spiral?

October 11, 2013

Visualizing an Ekman spiral using a deck of cards. To state this right upfront: this post will not explain why the surface layer is moving at a 45 degree angle…

Standing waves.

October 6, 2013

A seesaw to visualize how standing waves move in an enclosed basin. In enclosed basins, standing waves can occur. In the simplest case, they have a node in the middle…

Progressive waves on a rope

October 5, 2013

Visualization of progressive waves: wave form and energy move forward while the rope itself stays in place. When I talked about waves in GEOF130 recently, in order to explain the…

Why melting sea ice does not contribute to sea level rise.

September 29, 2013

Simple experiment on why the impact of glaciers and sea ice on sea level, respectively, are not the same. It could be so simple: An ice cube sinks into water…

Tasting sea water reloaded

September 25, 2013

Doing the “tasting sea water” activity again with a different group of students. A very good introduction to the concept of salinity is the “tasting sea water” activity. Last time…

Internal waves in a bottle

September 18, 2013

Internal waves are shown in simple 0.5l bottles. Waves travel on the interface between fluids of different densities and the phase speed of those waves depends on the density difference…

How mountains form

September 17, 2013

A very simple visualization of rock folding. See? When I said “very simple” I meant “very simple”. But it does help explain why sometimes rock layers are not nice and…

On the structure of fresh water and salt water ice

September 11, 2013

More details on the structure of fresh water and salt water ice. Fresh water and salt water ice have very different structures as I already discussed in this post. In the…

Melting ice cubes – what contexts to use this experiment in (post 4/4)

September 9, 2013

What contexts can the “ice cubes melting in fresh water and in salt water” experiment be used in? As you might have noticed, I really like the “ice cubes melting…

Melting ice cubes – one experiment, many ways (post 3/4)

September 7, 2013

Different didactical settings in which the “ice cubes melting in fresh and salt water” experiment can be used. In part 1 and 2 of this series, I showed two different…

How much salt is there in sea water?

September 6, 2013

Visualization of how much salt is actually contained in sea water. When preparing “sea water samples” for class, it is always astonishing to me how much salt I have to…

Properties of sea ice and fresh water ice

September 5, 2013

Sea ice and fresh water ice have distinctly different properties that can easily be investigated even in big class rooms. In “on how ice freezes from salt water” I talked…

Ice cubes melting in fresh water and salt water (post 2/4)

September 4, 2013

The “ice cubes melting in fresh water and salt water” experiment the way I usually use it in class. — Edit — For an updated description of this experiment please…

On how ice freezes from salt water

September 2, 2013

I’ve been wondering how to best show how sea ice freezes for quite a while. Not just that it freezes, but how brine is rejected. By comparing the structure of…

Ice cubes melting in salt water and freshwater (post 1/4)

September 1, 2013

Experiment to visualize the effects of density differences on ocean circulation. This is the first post in a series on one of my favorite in-class experiments; I have so much…

Forskningsdagene are almost upon us

August 30, 2013

Preparations for experiments to be shown at the science fair “forskningsdagene” are under preparation. Forskningsdagene, a cooperation between research institutes and schools, science centers and other educational places, will take…

And even more on density

August 28, 2013

My favorite experiment. Quick and easy and very impressive way to illustrate the influence of temperature on water densities. Today in the “introduction to oceanography” (GEOF130) we conducted my favorite…

More on density

August 28, 2013

Extremely simple experiment to illustrate the effect of density differences. At room temperature, will coke cans float or sink in freshwater? And how about coke light? Btw, this experiment is…

Tasting sea water

August 28, 2013

Hands-on activity on sea water salinity In the first lecture of the “introduction to oceanography” GEOF130 course 2013, we investigated water samples from four different regions: The Mediterranean, the tropical…

Category: demonstration (easy)