Category Archives: observation

Total internal reflection

Leave a reply

In the “static apnea” discipline in freediving, many cool pictures of athletes are taken underwater in a way that plays with the reflection of the athlete in the still water surface. This can lead to pretty spooky pictures (like the one of Victor in the top left). We do have other experiences with water, where there are areas where we can look in (or out), but then others where we can’t: In the bottom left, you see Mats and his shadow, even the individual tiles very clearly in the water. But the further back you look, the more you notice that the picture was taken from outside the water, because you start seeing more reflections in the water surface. In the bottom right, taken from within the water, you see reflections of all the divers and the lane markings in the surface except right at Edvin’s elbow, where we look out of the water and see what’s happening above the pool. And then in the top right, we don’t see the water surface at all — the only reason we know we are looking at Alex from within the water is that there are bubble rings floating between us and him. So what is going on here?

Continue reading →

Solar eclipse!

Leave a reply

The effort that went into today’s solar eclipse is nothing compared to the one in 2015, when we made it the topic of a workshop on how to use PBL in teaching (where the second session was happening exactly at the time of the solar eclipse, so we made it the topic of our case, which resulted in lots of different creative ways to actually watch it).

Today, we “just” relied on the protective glasses we had from last time, and — super cool idea that I first saw somewhere on Twitter — a colander, which gave us many mini suns, each with their own eclipses. #KitchenAstronomy!

Sadly, the pictures didn’t turn out so well — the edge is not sharp at all. But on a #WaveWatching blog, that’s actually not a bad thing: It just shows that light behaves like a wave and that even though it arrives in parallel rays at the colander, it spreads after going through the holes, thus blurring the edges. Diffraction is pretty awesome! And #WaveWatching is still the best way to learn about optics ;-)

Insta takeover on snowflake formation

Leave a reply

Back in December, I did a takeover of the Instagram account of WissKommSquad, a community of german science communicators. I translated it over new years, but somehow never published it. I have since taken tons of much better pictures of snowflakes, but the story I’m telling here is still interesting, I think: How snow and ice form through different processes and why they look the way they do. Have fun!

(First an embedded version directly from Canva, which I used to produce the story, and then below the cut the individual pictures)

Snow Story @SWissKommSquad by Mirjam Glessmer
Continue reading →

Marine energy: Tides. A guest post by Manel Camacho

Leave a reply

Today’s guest post is brought to you by Manel Camacho. Manel and I met on Twitter and bonded over our joint love of wave watching — me as a dedicated amateur, Manel as PhD student in marine energy. Today, Manel is giving us a glimpse into what marine energy is all about. Enjoy! :-)

—

As a person that grew up in the coast of a tropical country will be weird for me to say that I was afraid of the sea during most of my childhood. I remember going outside of our parked car at the sand to meet the sea, was my 1st time and the day was warm; no clouds anywhere and no wind. Same moment an enormous wave came into my direction, I ran inside and never went out for all day.

Ironic as it is despite this fear, 25 years later I was doing a Ph.D. on marine energy. Marine energy engineering is the subject that involves the use of our oceans to produce electricity, the sea by itself it is involved in one of the biggest energy exchanges on the planet earth. The energy exchange involves the gravitational pull of the sun/moon and also the sun thermal radiation.

The first force that I will talk about causes a phenomena called “tide”, as we know the moon and the sun can exert a gravity force over the earth. The gravity force as we know tries to pull out any mass into its direction, as the continents and the sea bottom are made of dense rock they resist this pull; however the seas can deform more easily, the force will pull out the seas above its normal level. This rising and decay of the sea level is called “tide”. The difference on elevation from the low level to the higher level can be over half a meter in open ocean, when its pulled is called “high tide” ad when its not “low tide”. 

We might think that half a meter of difference is not too much, but when the ocean reaches a depth of more than 3000m is considerable. Comparing lets take a circle of 1 meter radius in the sea and lift it 1 meter, we’ll the same force to do this is to pull up almost 95 liberty statues just one meter above the ground.

Now that we know how much force is need it to pull that single cylinder of water, imagine again the force necessary to make an entire ocean to vary half a meter on level. The forces of the sun/moon will cause the ocean to bulge, then earth rotation will cause these bulges to move across the globe. When we are at the coast and we see the water rising at night and day, what we see is the water reacting to these forces creating this massive but imperceptible lumps in the ocean.

The water height increases more at the coast than in open sea, this will cause that certain parts to rise several meters at the “high tide”. These sudden increases on water will cause a flood on the coast, if it moves to the coast is called “flood” or away from the coast “ebb”. These flows will cause strong currents in certain locations, these currents work similar to the wind blowing; the currents produced then can be used to harvest energy, the easiest way to do it is using a device similar to a wind turbine.

Devices used to extract energy from the tidal stream currents are called, tidal stream turbines. These devices use knowledge learn from disciplines as wind energy, marine, civil and offshore engineering as naval, mechanical and aerospace areas.

As any new device to produce energy many problems need to be solved, problems related to: how it affects to the animals, to the people and its way of living, how they will survive in extreme weather and many many more. But thats something to discuss further.

New #WaveWatching series happening over on Elin’s blog: #BergenWaveWatching!

Leave a reply

Kjersti, Steffi, Elin and I recently discussed ways to better integrate the GEOF105 student cruise into the course. Right now,  even though students write a report about their work on the student cruise, it’s pretty much a one-off event with little connection to what happens before and after, which is a pity. Having a whole research ship for a whole day for a group of 6-8 students (or possibly 10 next year) is such an amazing opportunity! We want to help students make the most of it by attempting to foster a curious mindset before they board the ship.

One idea is to ask the students to observe things throughout the whole duration of the semester, and then have them relate their own “time series” of those observations with what they observe on the student cruise. Ideally, students will be observing their chosen topic for a couple of weeks before the cruise, then go on the cruise looking at everything there with a focus on that topic, and then continue to observe it in their daily lives after the cruise. But even if it’s not connected to the student cruise or this specific class, I think giving students the task to make regular observations over the course of a whole semester would be a really good way to connect their studies better with their regular lives outside of university.

Do I have ideas of what the topics could be? Of course! And I have scheduled posts over the next two months, in which my ideas will be presented one by one. But today, I want to talk about what I think what purpose this assignment would serve.

The goal is not to collect data that will advance science or to work on original research questions. It is rather to help students get into the practice of focussing on details in the world around them that might otherwise go unnoticed. To collect observations using only minimal resources (like for example stopping on their commute for seconds only, taking pictures with their smartphones, using the readily available weather forecast for context). To try and explain pattern they observe using their theoretical background from university. I want to help students get into the habit of actively observing what is going on around them, to become fascinated with discovering things related to their studies in their everyday lives.

I myself, for example, am absolutely fascinated with waves, and I notice them anywhere (read more about that on my blog, if you are interested). On the most recent GEOF105 student cruise, there was a bucket that was used to bring seawater up on the deck for salinity to be measured. And what jumped out on me? The standing waves in that bucket! You see them in the picture below, but what struck me was that most people really didn’t seem to notice what was going on there, and how FASCINATING it was. Someone even commented to the effect that they would have never noticed the waves in the bucket if I hadn’t pointed them out to them, even though they were sticking probes right into the waves. And while I spent the better part of two days moving the bucket around to see all the different wave pattern that occurred on different spots on deck, most other people didn’t even seem curious to find out why myself and a handful of other people were staring into a blue plastic bucket. And that makes me sad. Does everybody need to find waves fascinating? Of course not. But should students at least be a little curious about science topics that clearly fascinate their instructors? Yes, I believe so.

More about the cool waves in the blue bucket in this blog post!

So my mission with this series of blog posts is to give examples of where you can easily observe oceanography-related phenomena in and around Bergen, hoping that you might start looking at those spots with different eyes. And maybe you will find a specific topic that you become fascinated with. Because once you start focussing on something that seems random and rare, the very thing seems to appear everywhere in your daily life. Like for example hydraulic jumps. As shown in the picture below — once you start focussing on those, you see them appear everywhere as if out of thin air.

Hydraulic jumps. Picture from this blog post

This kind of curiosity around physics phenomena is — in my opinion — absolutely desirable, especially in students. It makes dry theory or seemingly obscure topics become more relevant. As you start noticing phenomena, you also start noticing more about them, for example understanding the conditions under which the appear. And you also start anticipating where they might occur, so you will look to see whether your prediction is correct. It’s a vicious circle, but one that I would encourage you — and especially students — to enter. To me, it’s part of my identity as a scientist — to use my initial understanding of processes to continuously want to learn more and more about them.

Wave watching has definitely become a part of my life that I don’t want to miss. What will you start seeing everywhere? Or what is it that you are maybe already seeing everywhere that most people don’t? I am anticipating that my suggestions in this #BergenWaveWatching series will be strongly biased towards #wavewatching, so if you have any other suggestions (maybe even with pictures already?), I would love to hear about them! :-)

…and check out the #BergenWaveWatching series here!

Fog showing stream lines around cruise liner

1 Reply

Whenever I get out of my house and it looks like this, I am slightly disappointed because it means that the wave watching that morning will not be ideal. I mean, I like colorful sunrises as much as the next person, buuuut…

Today, at least, the fog was kinda interesting, also because there was a large cruise ship driving through.

There was a low layer of fog, but look at what happens as the ship passes through: It lifts up! Visualizing the stream lines around the obstacle. Pretty cool! (And thank you, little police boat, for making at least some waves for me today!)

Even better visible below, but check out the smoke coming from the ship’s chimneys. Do you see how it is propagating forward? Or does it just look like that to me? At least below the fog layer there was pretty much no wind. So what’s going on up there? Anyone care to explain?

Lüneburg — how a few centimetres in distance separate two seemingly completely different bodies of water

Leave a reply

Sightseeing is best when it involves a little water watching, like for example last weekend in Lüneburg.

Doesn’t it look intriguing below, the change from a calm, mirror-like surface to something a lot less regular on the other side of the bridge?

Take it in: so peaceful! Although, judging by the plants growing in the water and by how they look like someone took a rake and put them in order, there must be a substantial current going through underneath the bridge.

And turns out there is: The bridge is a weir and there is a waterfall on the other side!

I find it so fascinating how the appearance of water can change literally over the distance of a few centimetre. So calm on one side, and boiling, spraying, turbulent on the other!

And then just a couple meters further downstream, we are back to mainly calm and only a few bubbles floating along give you an indication of what just happened upstream…

And again, no matter how peaceful everything looks here, the water plants tell us that there is still a lot of water moving, bending the leaves with it.

Do you look at this kind of things when sightseeing, too?

Watching the tides cause an hydraulic jump in the Irish Sea!

Leave a reply

Looking at the picture above, taken in the South Walney Island Nature Reserve on our walk yesterday, what is the first thing you notice?

For me, it is not the cute little hide which is a perfect spot for seal and bird watching, for me it is — obviously! — what is going on with the waves! So much so that I spent the better part of an hour looking at the opposite direction of where all the seals were frolicking in the waves (except for one that came and played in the most fun part of the sea — more about that later).

Looking at the picture below, do you notice how different the different areas of water surface look? To the left of the wave breaker and going offshore from there, the surface is quite rough, with many waves of different wavelengths. But then going directly offshore from the wave breaker, the surface is smooth(er)! Followed by a rougher stripe, before it becomes smooth again, and a couple of well-defined wave crests reach the shore.

Zooming in on that area right off the wave breaker, you see that there are actually waves breaking towards the smoother area, away from the beach. Any idea what’s going on here, what might be causing those waves? (Hint: Even though there is a boat in the background, it is not some ship’s wake!)

What we can observe here is actually a pretty cool phenomenon, called a hydraulic jump. Due to the tide going out, there is a current developing around the tip of Walney Island, going from left to right in the picture above. This current goes over the still-submerged part of the wave breaker. Since the cross section through which the water has to squeeze is all of a sudden a lot smaller than before and after, the water has to accelerate. And it accelerates so much that waves traveling on it are just flushed downstream and the surface looks smooth(er). Only when the cross section is wider and the water has slowed down, waves become visible again.

The spot where waves are exactly as fast as the current, but running against it, is called “hydraulic jump”. You can spot it right where the waves are breaking: They are trying to go back upstream but don’t manage to, so they stay locked in one place (see here for an analogy of people running up and down escalators to explain this phenomenon). You do see hydraulic jumps “in the wild” quite often, for example in rapids in rivers (and even more so in regulated rivers, very nice example here!). In case of the hydraulic jump right here, there was a seal playing in the current, clearly enjoying the wave action (and quite possibly also feeding on poor fish that suddenly get swept away with the current).

And indeed, 20 minutes later, the same spot looks like this: the surface roughness is a lot higher towards the right of the wave breaker, but all in all there are much fewer, and much smaller waves.

And another 20 minutes later, the formerly submerged wave breaker is revealed!

I find it always so cool when you see a wave field and just from what that wave field looks like, you can deduce what the ground underneath has to be like! In this case from seeing the hydraulic jump, you know that the wave breaker has to continue on offshore.

Wanna see the whole thing in action? Then here is a movie for you!

https://vimeo.com/348247842

And the coolest thing is that this spectacle will repeat with every outgoing tide, so pretty much twice a day! And I am fairly confident that it will also happen halfway between, again, when the tide comes in and the current goes in the opposite direction. I would love to go back and check!

Enjoying the South Walney Island Nature Reserve

2 Replies

Wanna come on a walk with me and Astrid around the southern tip of Walney Island?

This is what our parking spot looked like when we arrived (we did park on this side of the gate, obviously).

I find the salt marshes so impressive — all that grass that gets flooded every 12 hours! At low tide I keep taking pictures of crabs and little sea critters that got stranded in grass.

But very nicely visible how important the grass is for coastal protection: Waves get dampened out pretty quickly if they are running through grass!

But let’s start walking. See the high tide lines on the beach? Great markers of some of the last high waters. This kind of stuff — parallel lines in the sand, mirroring the water line — looks very calming to me!

In the South Walney Nature Reserve, there are several hides where you can sit and bird (or seal) watch, or enjoy the shade or shelter. They are so lovingly done, and all include information about the wildlife to be observed. One even has an exhibition of the different sands found in different locations around the island!

…and about other stuff found on the beach: beach shingle, rabbit poo and cow dung! I love this!

Moving on, we got closer to the lighthouse, which, unfortunately, isn’t open to the public any more. Just imagine the kinds of views you would get from up there!

And then, as we were approaching another hide (the red cabin in the picture below), I spotted something else that held me captivated for the better part of an hour. And I don’t mean the seals frolicking in the sea! Can you spot it?

Here is a closer look. Do you see what is going on there?

I’ll publish a blogpost with the explanation later today (it just got too much to put into one post), so stay tuned if you want to look more closely at the water with me!

Walking back, here is a view of an old castle ruin across the bay. See the now exposed salt marshes and gullies?

And here we are, back where we started. Go back to the picture up top of this same gate — isn’t it amazing that all this grassland was flooded only a couple of hours earlier, and will be flooded again in just a couple of hours? I am so used to seeing the german Wadden Sea coast where low tide exposes nothing more but mud…

An art & science collaboration with Wlodek Brühl: #dropphotography

1 Reply

If you are here because you saw my title or talk at the Science in Public conference in Manchester and are curious about #dropphotography as a form of art&science collaboration in scicomm — a special welcome to you! If you are here for any other reason — welcome anyway! :-)

One of my favourite pet projects right now is the #scicomm collaboration with the artist Wlodek Brühl.

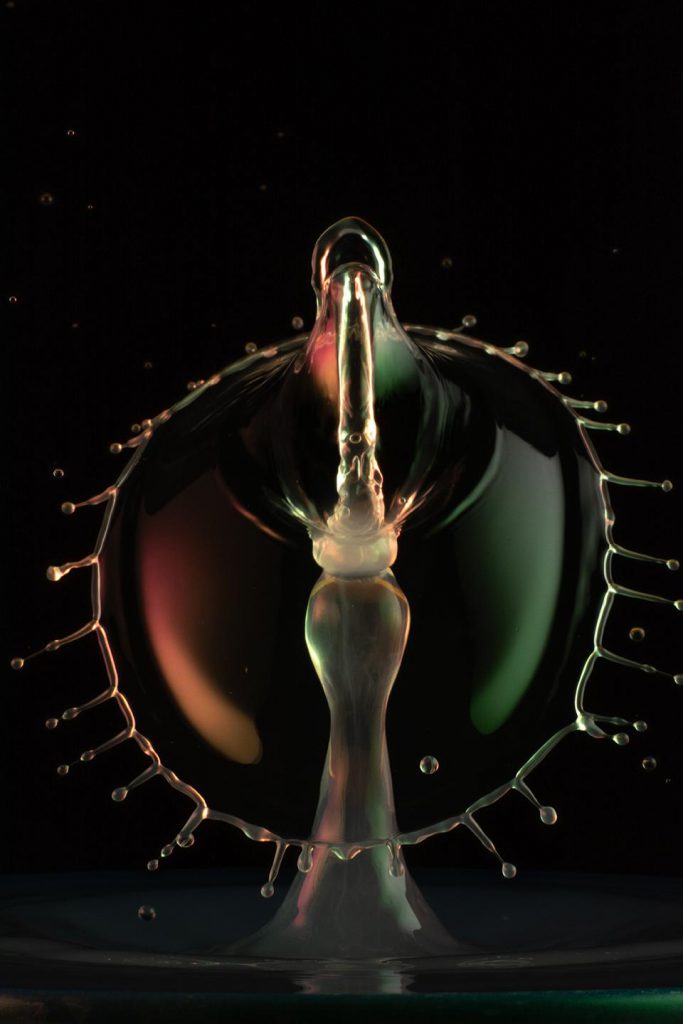
The idea behing the collaboration is very simple: Wlodek does awesome drop photography like what he showed in his recent exhibition, or the picture below: Drops falling into water, creating sculptures that he captures with digital photography.

I, on the other hand, use the opportunity of having people fascinated and mesmerised by this art, and curious to learn more about it, to talk about — what else? — physics! :-)

For one example of what that collaboration looks like in practice, check out my speech at the opening of his latest exhibition. We have a workshop coming up this autumn that we will run together, as well as other exciting projects which are, unfortunately, still secret. It’s going to be awesome, though!

But back to physics: Creating the exact sculpture you want requires enormous precision. This is what the setup looks like: Reservoirs above a vessel in which the drops fall. And a complex setup of flashlights and a digital camera, all coordinated by a custom-made piece of software.

The most important thing influencing the momentum with which a drop hits the water below is the height it falls from. Below, pictures are taking at constant intervals after drop release, yet you see that the for each new picture, the drop fell a little further than it did in the previous interval — it fell a little faster due to acceleration of gravity. Thus the longer you let a drop fall (i.e. the higher the drop falls from), the more it will accelerate, bringing more energy into producing a fountain.

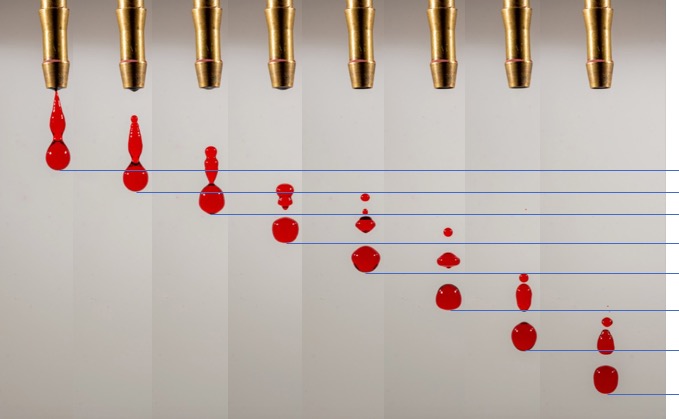
The next thing that needs to be very precisely controlled are the opening times of the valves that release the drops. Not only when they open, but also for how long. Consider opening times of the valves in the picture below, left to right: 50, 55, 60, 70  milliseconds (The series of pictures on the left you know already from the “acceleration of gravity” pic above).

Depending on how long the valve is opened, different volumes of water are released, forming different drops. Easy to imagine that this will lead to different fountains once the drops hit the water below!

So what happens exactly once the drop hits water? The water surface gets deformed as the drop pulls it downwards. Due to surface tension, it then bounces back up, bringing up a column of water, that then collapses back down. And all these disturbances radiate ripples away from the original point of impact — capillary waves! (Capillary waves are super interesting because they behave very differently from “normal” gravity waves, but that’s a topic for a different post!)

But so that’s how fascinating it is to watch just one drop falling into water. Now imagine several drops falling one after the other, such that a second or third drop hits the column rising up after the first drop already hit the surface? That’s what makes these interesting umbrella shapes:

As you can imagine, there are tons of parameters you could vary now. Not only fall height and drop size, time lag between drops, number of drops that fall, but also viscosity of the fluid, shape of the bowl the drops fall into, all kinds of things. And that’s only using the easiest setup! You could also imagine using several valves, or air pressure to shoot drops with more momentum, or even have water shooting up from below (all of which Wlodek has done!).

And then, of course, depending on when exactly you choose to take a picture of the sculpture, you will see it in very different stages of formation and decay. You see the attempt of surface tension to minimise disturbances, instabilities that still form along the rim of the umbrellas which ultimately burst into many different small droplets…

Do you see the potential to talk about physics pretty much forever here? I love it! :-)