A very convenient way to describe a flow system is by looking at its Froude number. The Froude number gives the ratio between the speed a fluid is moving at, and the phase velocity of waves travelling on that fluid. And if we want to represent some real world situation at a smaller scale in a tank, we need to have the same Froude numbers in the same regions of the flow.
For a very strong example of where a Froude number helps you to describe a flow, look at the picture below: We use a hose to fill a tank. The water shoots away from the point of impact, flowing so much faster than waves can travel that the surface there is flat. This means that the Froude number, defined as flow velocity devided by phase velocity, is larger than 1 close to the point of impact.
At some point away from the point of impact, you see the flow changing quite drastically: the water level is a lot higher all of a sudden, and you see waves and other disturbances on it. This is where the phase velocity of waves becomes faster than the flow velocity, so disturbances don’t just get flushed away with the flow, but can actually exist and propagate whichever way they want. That’s where the Froude number changes from larger than 1 to smaller than 1, in what is called a hydraulic jump. This line is marked in red below, where waves are trapped and you see a marked jump in surface height. Do you see how useful the Froude number is to describe the two regimes on either side of the hydraulic jump?
Obviously, this is a very extreme example. But you also see them out in nature everywhere. Can you spot some in the picture below?
But still, all those examples are a little more drastic than what we would imagine is happening in the ocean. But there is one little detail that we didn’t talk about yet: Until now we have looked at Froude numbers and waves at the surface of whatever water we looked at. But the same thing can also happen inside the water, if there is a density stratification and we look at waves on the interface between water of different densities. Waves running on a density interface, however, move much more slowly than those on a free surface. If you are interested, you can have a look at that phenomenon here. But with waves running a lot slower, it’s easy to imagine that there are places in the ocean where the currents are actually moving faster than the waves on a density interface, isn’t it?
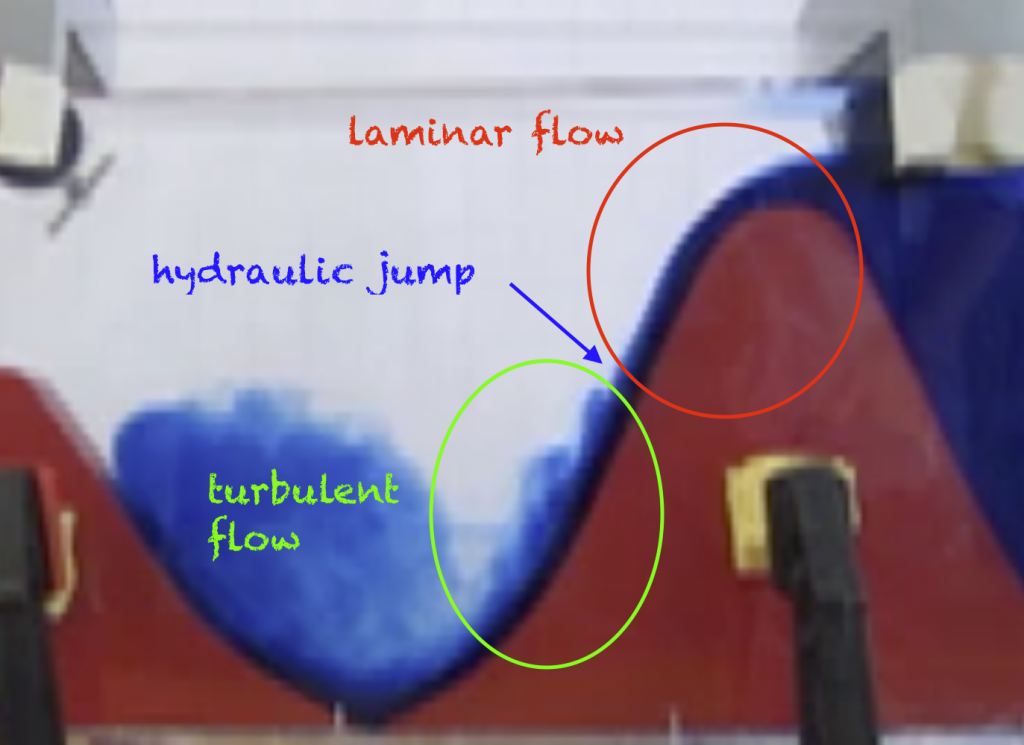
For an example of the explanatory power of the Froude number, you see a tank experiment we did a couple of years ago with Rolf Käse and Martin Vogt (link). There is actually a little too much going on in that tank for our purposes right now, but the ridge on the right can be interpreted as, for example, the Greenland-Scotland-Ridge, making the blue reservoir the deep waters of the Nordic Seas, and the blue water spilling over the ridge into the clear water the Denmark Strait Overflow. And in the tank you see that there is a laminar flow directly on top of the ridge and a little way down. And then, all of a sudden, the overflow plume starts mixing with the surrounding water in a turbulent flow. And the point in between those is the hydraulic jump, where the Froude number changes from below 1 to above 1.
Nifty thing, this Froude number, isn’t it? And I hope you’ll start spotting hydraulic jumps every time you do the dishes or wash your hands now! :-)
I am really enjoying this blog. I am trying to understand hydraulic jumps. Can you explain why faster flowing water slows down? Friction? ( I thought water flows had negligible friction). Collision with slow water?
But how is this maintained? And how does fast flowing water entrain slower water? Is turbulence required? And finally, are hydraulic jumps really any different from standing waves? Do the former just have enough energy to break upstream?
Hi Joe, Thanks for your comment! Always makes me happy to read people are enjoying my blog :-)
There are a lot of reasons why the water might be slowing down. You mention two: Friction, but probably with the boundary or the bottom, and collision with slower water are definitely important! Other reasons might include for example a sudden opening of the cross section of the flow (if the same amount of water suddenly has to fill a larger cross section, it has to slow down), a change in the slope of the bottom (if water isn’t accelerated any more by a sloping bottom, or even has to go up hill, it will slow down).
I don’t quite understand what you mean about how it is maintained?
When fast water is flowing through slow water, there is going to be some friction between the two, which will lead to disturbances of the boundary between the two, i.e. turbulence. And that will then entrain water.
In my mind, hydraulic jumps and standing waves are very much linked: In a standing wave, the wave’s phase velocity is exactly as fast as the current underneath, which is why the wave stays in place. The hydraulic jump is the spot where the phase velocity changes goes through exactly the same velocity as the current, so if that happens over a longer stretch of water, you will have a standing wave there: A wave that is caught because it is too slow to move upstream against the current, but also to fast to be washed away downstream with the current. In case of the water hose in the post above however, there is the area around where the water hits the floor where the water is moving a lot faster than a wave’s phase velocity, and then over a really short distance the water’s speed changes from faster than phase velocity to slower than phase velocity, hence a distinct hydraulic jump. Does this make sense?
Yes, thanks that makes sense. Is there a simple explanation for why hy a river wave never moves upstream? ( At least I have never seen this except with a tidal bore). Waves with more speed seem to change from a smooth standing wave to a steeper wave then a breaking wave, but never move upstream against the current.
My question about how a collision with slower water is maintained is to do with this quandry: why does a body of water moving at speed not push the slower water out of the way and create a path of faster moving water through the slower water? I would expect this to happen with other moving objects. If friction is low in water, why does water moving down slope slow so quickly? Newton’s laws suggest it would keep moving, even if the slope flattened out, until it was acted on by a force like friction. But water does not seem to make a path for itself. Is turbulence between the two bodies of water (like the fast moving water entering a slow pool) the main source energy loss?
I am really enjoying thinking about this – I used to kayak obsessively, these days I body surf, and I completed a PhD in marine biology a few years ago, so water has been a big thing in my life, but I have never studied the physics of water. I live in New Zealand which has some great standing waves and hydraulic jumps.
Thanks again, Joe.
Hi Joe!
A wave can only move upstream if its phase velocity is larger than the velocity of the current that it is moving against. So if you have a slowly moving river, then it is definitely possible for waves to go upstream. Think of the mouth of the river where it meets the ocean — technically, you are still in the river and the water is flowing out into the ocean, but swell from the ocean can propagate into the mouth for a bit. And tidal bores do basically just that: propagating against the current with a phase velocity that is higher than the velocity of the current.
To try and answer your question: To a certain degree the faster water DOES push the slower water out of the way. But think about billiard for a second: two equal balls on a flat surface, one at rest and one moving at a given velocity. When they collide (assuming that you hit the ball right in the center), what happens is that the ball that was at rest now moves at (pretty much) the velocity the other ball was moving at, and that the ball that was moving is now still in the spot where the two balls collided. The momentum got transferred from one ball to the other. And almost the same thing happens with the water, too. Of course, two bodies of water don’t just collide and then one bounces away and the other one stays at rest; there is mixing going on etc.. But the physics are the same in so far that one volume of water moving at speed can’t just hit a second volume of water and make it move at the same speed. Either all of it starts moving, but then more slowly, or some of it continues to move and the rest stays put (and the proportions of that depend on the topography in which this is happening). So friction does cause some energy loss, but also, more importantly, it isn’t even about energy lost: the energy of the system is only enough for one of the bodies of water moving at the initial speed, or both of them moving a lot more slowly. Does this make sense? I think I might have a different picture in my mind than you do, maybe if you have an image it’s easier to talk about what’s really going on there?
I love kayaking! Although I suck in white water, I find it super scary. But I used to play canoe polo and that is so much fun! And I’d love to visit New Zealand at some point, I have heard the most amazing things! Best, Mirjam
Thanks Mirjam, that makes sense and the billiard ball analogy is a good one. I think I was thinking that if I have a large number of billiard balls, and I am shooting at a group of stationery balls at the other end of the table, then eventually I would be able to knock all the stationery balls out of the way and create a path that my fast moving balls could move through without collisions. So in a river I would expect to have a fast current down the middle of the river and slow or still pools on either side. But instead rivers at normal flow tend to speed up (where the gradient is steeper, forming rapids) then slow down (at a hydraulic jump or the pools between rapids).
Swollen or flooded rivers often do move at fairly constant speed – the speed is similar bank to bank and for long stretches of river. I have also seen this in a kind of “river without banks”. I was kayaking across Cook Strait (between the North and South Islands of New Zealand). It was a still day and the sea was flat and glassy. But Cook Strait is funnel shaped in three dimensions – there is a wide deep area to the south-east, and a narrow shallow area to the north-west. This makes for some impressive tidal currents. What was strange was that the tidal currents formed a distinct “river” in the sea. In a few kayak lengths I went from flat, glassy, apparently still water into a river of fast moving (at least 5 knots) water with large (1-2 metre) standing waves). The “river” was maybe 100 metres wide, and after several minutes of hard paddling I crossed the “river” to the other side – more still glassy water. I don’t know how far this current extended, probably 10s of kilometres.
So can I try and answer my own question: If there is sufficient energy – in a flood state river or a tidal current (the one I am describing must have been several thousand cumecs) there is enough energy for most of the water to gain speed and maintain it. In a normal river turbulent interactions with slow moving water in eddies and pools transfers energy from fast to slow water decreasing the speed of the main current. Does this make sense?
But now I am wondering about the interactions between the fast and slow water in a normal river. Even if the velocity of the water at the steep part of a rapid is more or less linear – directed straight downstream, the water will slow down and push sideways into an eddy or become turbulent at the eddy-line. It seems almost non-newtonian for the linear water to start pushing or swirling towards still water at the sides of the river – as if the billiard balls not only hit the stationary balls directly in their way, but curve towards balls lying to the side and entrap them. This would make sense if there was friction between the fast moving and stationery balls, but I am used to thinking of water as having very little friction. So why does waterin a current apparently curve to the sides?
Thanks, I love your blog.
Hi Joe, Thanks for your reply, I love this conversation! :-)
I guess the billiard ball analogy only carries so far. One thing that it doesn’t include is continuity, which we do have in the river. In your example, yes, you can kick all the stationary billiard balls away and get a path for the fast moving ones. In the river, however, every water parcel you kicked away will be replaced by another one (since you don’t just create empty space in the river the way you do on a pool table). Therefore, you can’t just get rid of a parcel of water one after the other. For every one you got rid of to clear your path, there will be a new one coming in from the sides or from underneath or wherever (depending on the topography and situation).
And since you really dislike thinking about friction in water: This effect — water coming in from the sides — also creates a link between the fast flowing and stationary parts of the river, since water coming in from the sides will have to speed up to join the moving water. And even if you were moving water almost as if through a pipe, so in a confined flow, what will happen is that there will be sometimes instabilities in the flow; meanders, parts slowing down a little more, that kind of thing. And every bend in the current will be filled with slower water from the side, and as more fast water pushes from upstream, the slower water will speed up a little, creating more disturbances behind it where now more slow water will be sucked in to replace it. And this is exactly what creates turbulence, eddies, and behaves a lot like friction, except on a larger scale, not on a molecular one. So in oceanography, we’d still think of it as friction and parameterise it as friction in numerical models. Does this make sense?
The tidal current you describe sounds fascinating. If I had to guess, I’d say that the river without banks was coming through the narrow end of the tunnel, moving out the wider part? And if I had to guess further, I’d say that the fast-flowing river was slowing down and widening the further you got away from the narrow end of the funnel — albeit probably very little. For a situation where the water moves through the funnel “the right way”, I’d suspect that there would be a faster current right upstream the narrowest part of the funnel, but that overall the flow would be a lot more sluggish and over a much wider part of the funnel. I’d love to go there now to check :-)
Mmm, Thanks, yes that all makes sense, but after a long break I have hit on the crux of my problem – I have to ask you this otherwise it will keep me up at night!
The conventional explanation I have heard for the jump is that the water slows down, losing kinetic energy and this is changed into potential energy through a rise in height. That is fine, but if the water is slowing down because it is losing energy through collisions that transfer of energy to slower moving water etc., then why is energy left over to be changed to potential energy? This implies that the water is slowed down by some process other than loss of energy, with the surplus kinetic energy having to change into potential energy – i.e. height.
The explanation seems circular – the jump is created because the water slows down, the slowing down is caused kinetic energy transferring to other water. So why does some energy get changed to potential energy and not just act to move more stationery water out of the way?
It is as if a moving billiard ball hits a stationery billiard ball, and not only accelerates the stationery ball – as expected – but also jumps into the air. I can understand this happening if the moving water is hitting stationery water at an angle and is deflected upwards, but this is a simple collision which doesn’t need the “change in energy from one form to another” part of the explanation. Obviously anything moving upwards in a gravitational field loses kinetic energy and gains potential energy, but the conventional explanation seems to say that moving upwards is a consequence of energy loss, not a cause of energy loss.
Is this a semantic problem or confused phrasing, or does the water really slow down and therefore rise in height? Help Mirjam!
BTW I really enjoyed the dead water experiment posts. I haven’t experienced dead water but I know how frustrating it can be when the chop has just the wrong period for a vessel’s length. However hard you paddle your kayak you are always pushing against a wave ahead of you and can’t gain any more speed. Nansen must have experienced similar frustration.
Hi Joe,
I am loving this conversation! And thanks — we really enjoyed playing with the dead water experiments, too. So cool to see the internal wave slowing down and stopping a ship even though it’s being pulled with the same force that was sufficient to move it before!
I have heard the kinetic and potential energy explanation, too, but I am not too happy with it, either. Or, rather, in my head, I use a different explanation:
While you are in a super critical flow, the water is flowing faster than waves on it can travel, so all waves/disturbances are being flushed downstream and away. In a subcritical flow, however, waves can travel both up- and downstream without any problems. So I imagine the hydraulic jump (where the flow changes from supercritical to subcritical) as the place where all the waves that travel upstream in the subcritical part get “bunched up”: They are running as far upstream as they can, but then at some point the current velocity is so fast that they can’t compete against it and are locked in place running exactly as fast upstream as the current is carrying them downstream. And if all those waves are stuck in this place, in my mind it makes sense that the water level must go up (since there are all those waves accumulating there). Does that make any sense to you?
Another point about the water slowing down: That can happen due to friction as you describe. But it could also happen for other reasons: If, for example, you turn on the water in your sink when doing the dishes, the water hits the sink and then spreads to all sides, forming some kind of circle of supercritical flow, and then eventually an hydraulic jump and then subcritical flow, right? So the area that each segment of flow covers as it moves radially outwards gets bigger and bigger. Since the amount of water per segment stays the same, it has to move slower and slower as it moves outwards, since there is less and less water available to cover the sink’s floor. So eventually the water will move at the same speed as the waves (i.e. you’ll have the hydraulic jump) and then after that it’s subcritical. So in this scenario we don’t actually need to “loose” any energy at all, we just spread the same amount over larger and larger areas until something happens. Does this make sense?
Looking forward to hearing from you again :-)
Thanks Mirjam, I am so relieved that you are unhappy with the potential/kinetic energy explanation – It doesn’t work for me and your explanation is so much better. You are really good at this!
But – and I always have a but – now I need to know what is the source of the waves? and why do they usually stay in the same place? Here I am thinking of what I call a typical river rapid. The water accelerates as the gradient of the river bed steepens. In this part of the rapid the water flow is smooth, apparently linear, but at the bottom of the rapid there is a series of standing waves. This pattern it seems similar whether the river bottom is gravel, a rock shelf or a concrete weir.
What bothers me is that waves in rivers rarely move upstream, at least not visibly (I accept that a tidal bore is an exception). In turbulent, flooded rivers I can pick out undulations, maybe waves, being washed downstream, and I can accept that this is happening in any supercritical flow – but the waves don’t form clearly visible peaks until the velocity of the water changes to subcritical, where the wave energy would reinforce itself until a visible peak forms.
OK, but the typical series of standing waves do not move relative to the river bed. You can surf them in a kayak and you stay in the same place relative to the river bed. For this to happen the velocity of the wave must be upstream and equal to the velocity of the water downstream. I have always assumed that the speed of the wave is in some way determined by the speed of the current, just because standing waves in rivers are so common, whereas downstream or upstream moving waves are rare, not visible and not easily felt ( in a kayak you can sometimes feel a wave that’s not clearly visible).
So what is causing these waves, or the waves that form a hydraulic jump? Obviously irregularities in flow, or obstacles or whatever might propagate waves, but why do they so often propagate upstream at the same speed as the current?
On a more minor note I am a bit unhappy with the explanation with your suggestion that the water in a sink has to slow down as it spreads out. This seems anti-newtonian – surely the water molecules will move outward at a constant speed until acted on by another force (friction or something, according to Newton’s first law). If the water spreads out, as it must, surely it just gets shallower. At this scale I imagine friction with the sink bottom is quite important, but I also wonder about drag caused by polar forces. I can imagine in a thin layer these forces might act to pull the water together as the geometry of the flow causes it to spread out. Is this a source of drag? I always get a little uneasy when explanations suggest that something has to happen to a moving particle or something (I have similar problems with the usual explanations for lift produced by air flowing over an aircraft wing). It suggests that the particle somehow “knows” what is happening around it. In the sink example each particle has to “know” that the current is spreading out over a larger area. Surely each particle moves independent of the particles around it unless there are intermolecular forces or something?
It is the beginning of summer here in New Zealand and we have had a couple of days of very clean medium sized swell at the beach – great bodysurfing conditions so I have been spending a bit of time among waves. I’m very grateful for your help in intellectualising the experience!
Hi Joe,
Great to hear from you again! :-)
Let’s see if I can answer those questions. Phew! :-)
What’s the source of the waves? There can be several sources. A wave produced by any of the “normal” sources (wind, animals, boats, …) will get locked in place at the hydraulic jump because it can’t travel further upstream. But more relevant at the rapids is probably the shape of the ground underneath: Usually there is a rock or something that the water “jumps over” (similar to those mountain bikers jumping over the little hills — they drive up the slope and then somewhat overshoot at the peak before they land a bit down on the opposite slope). Or if the river suddenly becomes a lot more narrow, the water level might also have risen up before the narrowest bit, and then water “falls down” afterwards when the river widens again. The water overshooting the normal resting water level in either direction is a wave in itself, and then those two or three smaller wave crests downstream are descendants of that first one. Does that make sense?
“I have always assumed that the speed of the wave is in some way determined by the speed of the current, just because standing waves in rivers are so common, whereas downstream or upstream moving waves are rare, not visible and not easily felt ( in a kayak you can sometimes feel a wave that’s not clearly visible).” – Well, this depends on how you measure the speed of the wave. Relative to the current, the wave speed does not depend on the current, it is just moved with it. But then relative to the river bed, of course faster flowing rivers seem to have faster waves on them. And rapids are more easily spotted than “normal” waves, because they are locked in place and persist over longer times. Also typically rapids have a larger wave height than the other “normal” waves caused by wind or whatever (Wind-forced waves in rivers have to be quite small, because there isn’t a lot of fetch for the wind to put energy into generating waves. Animals or paddlers don’t put that much energy into making waves, either)
“… but why do they so often propagate upstream at the same speed as the current?” — Waves propagate in all directions simultaneously, but the part that is propagating downstream is a lot more difficult to spot than the one locked into place, because as it gets swept away, its amplitude is decreasing fairly quickly (since no more energy is supplied to keep it up)
“On a more minor note I am a bit unhappy with the explanation with your suggestion that the water in a sink has to slow down as it spreads out.” — You are right, that’s really not a good way of putting it. The volume flow per circle segment decreases as the radius of the circle increases. So as the water is spread out over larger and larger areas, it becomes shallower and friction with the bottom becomes more and more important. So that’s probably the mechanism there. I don’t think that molecular forces are important for slowing down the flow, but that’s just a gut feeling.
Is this making things any clearer? I need to think about this more, I am getting confused now (Which is awesome, I love thinking about this kind of stuff and don’t do it enough :-D)
Pingback: Please discuss: Experimental setup for Nansen’s “dead water” | Mirjam S. Glessmer
Pingback: My elevator analogy for Froude numbers | Mirjam S. Glessmer
Pingback: My escalator analogy for Froude numbers | Mirjam S. Glessmer
Pingback: Watching the tides cause an hydraulic jump in the Irish Sea! | Dr. Mirjam S. Glessmer