New article published! “Adapting a Teaching Method to Fit Purpose and Context” (Glessmer, Bovill & Daae; 2024), based on this blogpost, but a little more thought through and polished with Cathy and Kjersti in beautiful Voss! Check it out here, and enjoy!
M. S. Glessmer, C. Bovill, and K. Daae (2024). Adapting a teaching method to fit purpose and context. Oceanography, https://doi.org/10.5670/oceanog.2024.603.
I’m not a big fan of student evaluations of teaching, since they’ve often been shown to be biased (see for example Heffernan (2021)), so when I saw the title of this article on “What Students Value in Their Teachers – An Analysis of Male and Female Student Nominations to a Teaching Award” by Wennerberg et al. (2023), I dropped everything and read it, because suspected that they would find the same bias, as they did. Here is my summary.
Kjersti and I have been talking about asking students to take turns and write summaries of lectures throughout the whole semester. We would then give feedback on them to make sure we get a final result that is correct (and that the student learns something, obviously). The summaries are then collected into a booklet that students can use to study for the exam. I did that when I was teaching the “introduction to oceanography” 10 years ago and liked it (also great feedback for me on what students thought was important!), but in the end it is just one more thing we are “asking” the students to do, so is it really such a good idea?
Then on my lunchtime walk today, I listened to “lecture breakers” episode 78. Great episode as always! Early in the podcast several design criteria are mentioned, for example for intrinsic motivation it’s important to give students choice and show the relevance of what they are doing to their real life (more on the self-determination theory here), and that from an equity perspective, it’s important to provide different perspectives on a topic. Those stuck with me, and then one piece of advice was given: to let students adopt roles. Generic roles like a facilitator, researcher, devils advocate; or roles that are specific to the topic of discussion. They did not really elaborate on it very much, but what happened in my head is this: What if we combined our summaries with the idea of students choosing roles?
There are so many stakeholders in science, and students might have preferred approaches or might want to try on potential future roles. For example, someone could choose to take on the role of a minutes keeper and write a classical summary of the main points of a lecture. That would be all I asked my students to do back in the day, so not super exciting, but maybe it is what someone would choose? Or someone might choose to be a science journalist that does not only document the main points, but additionally finds a hook for why a reader should care, so for example relating it to recent local events. Or someone could pick the role of devil’s advocate and summarise the main points but also try to find any gaps or inconsistencies in the story line. Or someone might want to be a teacher and not only summarise the main points, but also find a way to teach them better than the lecturer did (or possibly to a different audience). Or someone might want to be a curator and combine the key points of the lecture with other supporting resources. Or an artist, or a travel guide, …? Or, of course, there are specific roles depending on the topic: A fisherman? Someone living in a region affected by some event? A policy maker? A concerned citizen?
Choosing such a role might give students permission to get creative. A summary does not necessarily be a written piece, it could also be a short podcast or a piece of art, if they so choose. That would definitely make it a lot more fun for everybody, wouldn’t it? No idea if students would like this new format, but it’s definitely something that I want to bring up in discussions, and — if they think it’s a good idea — also give a try some time soon!
One thing I really enjoy about teaching virtually is that it is really easy to address everybody by their names with confidence, since their names are always right there, right below their faces. But that really does not have to end once we are back in lecture theatres again, because even in large classes, we can always build and use name tents. And voilà: names are there again, right underneath people’s faces!
Sounds a bit silly when there are dozens or hundreds of students in the lecture theatre, both because it has a kindergarten feel and also because there are so many names, some of them too far away to read from the front, and also you can’t possibly address this many students by name anyway? In last week’s CHESS/iEarth workshop, run by Cathy and Mattias on “students as partners”, we touched upon the topic of the importance of knowing students’ names, and that reminded me of an article that I’ve been wanting to write about forever, that actually gives a lot of good reasons for using name tents: “What’s in a name? The importance of students perceiving that an instructor knows their names in a high-enrollment biology classroom” by Cooper et al. (2017). So here we go!
In that biology class with 185 students, the instructors encouraged the regular use of name tents (those folded pieces of paper that students put up in front of themselves), and afterwards the impact of those was investigated. What they found is that while of the large classes students had taken previously, only 20% of the students thought that instructors knew their names. In this class it were actually 78% (even though in reality, instructors knew only 53% of the names). And 85% of students felt that instructors knowing their names was important. It is important for nine different reasons that can be classified under three categories, as Cooper and colleagues found out:
So what does that mean for us as instructors? I agree with the authors that this is a “low-effort, high-impact” practice. Paper tents cost next to nothing and they don’t require any effort to prepare on the instructor’s side (other than it might be helpful to supply some paper). Using them is as simple as asking students to make them, and then regularly reminding them to put them up again (in the class described in the article, this happened both verbally as well as on the first slide of the presentation). Obviously, we then also need to make use of the name tents and actually call students by their names, and not only the ones in the first row, but also the ones further in the back (and walking through a classroom — both while presenting as well as when students are working in small groups or on their own, as for example in a think-pair-share setting — is a good strategy in any case because it breaks up things and gives more students direct access to the instructor). And in the end, students even sometimes felt that the instructors knew their names when they, in fact, did not, so we don’t actually have to know all the names for positive effects to occur (but I wonder what happens if students switch name tents for fun and the instructor does not notice. Is that going to just affect the two that switched, or more people since the illusion has been blown).
In any case, I will definitely be using name tents next time I’m actually in the same physical space as other people. How about you? (Also, don’t forget to include pronouns! Read Laura Guertin’s blogpost on why)
Cooper, K. M., Haney, B., Krieg, A., & Brownell, S. E. (2017). What’s in a name? The importance of students perceiving that an instructor knows their names in a high-enrollment biology classroom. CBE—Life Sciences Education, 16(1), ar8.
My new Twitter friend Kirsty, my old GFI-friend Kjersti and I have been discussing teaching in laboratories. Kirsty recommended an article (well, she did recommend many, but one that I’ve read and since been thinking about) by Buck et al. (2008) on “Characterizing the level of inquiry in the undergraduate laboratory”.
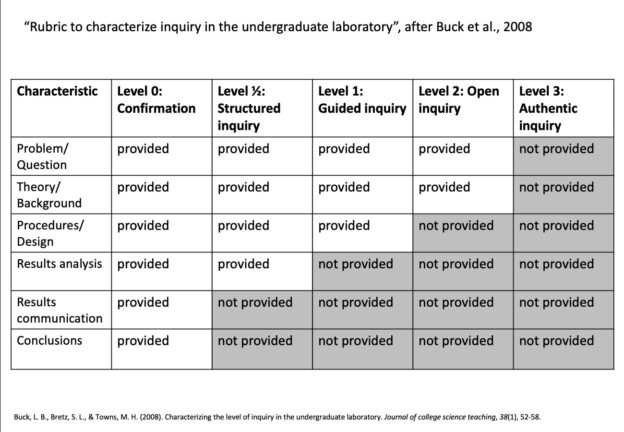
In the article, they present a rubric that I found intriguing: It consists of six different phases of laboratory work, and then assigns 5 levels ranging from a “confirmation” experiment to “authentic inquiry”, depending on whether or not instruction is giving for the different phases. The “confirmation” level, for example, prescribes everything: The problem or question, the theoretical background, which procedures or experimental designs to use, how the results are to be analysed, how the results are to be communicated, and what the conclusions of the experiment should be. For an open inquiry, only the question and theory are provided, and for authentic inquiry, all choices are left to the student.
The rubric is intended as a tool to classify existing experiments rather than designing new ones or modifying existing, but because that’s my favourite way to think things through, I tried plugging my favourite “melting ice cubes” experiment into the rubric. Had I thought about it a little longer before doing that, I might have noticed that I would only be copying fewer and fewer cells from the left going to the right, but even though it sounds like a silly thing to do in retrospect, it was actually still helpful to go through the exercise.
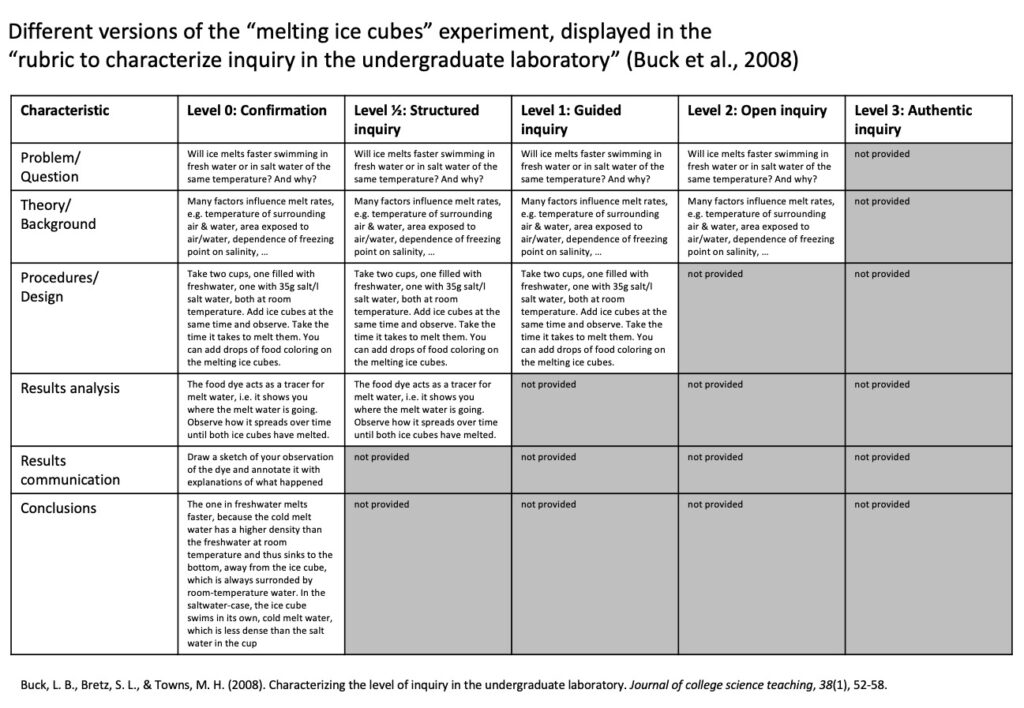
It also made me realize the implications of Kirsty’s heads-up regarding the rubric: “it assumes independence at early stages cannot be provided without independence at later stages”. Which is obviously a big limitation; one can think of many other ways to use experiments where things like how results are communicated, or even the conclusion, are provided, while earlier steps are left open for the student to decide. Also providing guidance on how to analyse results without prescribing the experimental design might be really interesting! So while I was super excited at first to use this rubric to povide an overview over all the different ways labs can possibly be structured, it is clearly not comprehensive. And a better idea than making a comprehensive rubric would probably be to really think about why instruction for any of phases should or should not be provided. A little less cook-book, a little more thought here, too! But still a helpful framework to spark thoughts and conversations.
Also, my way of going from one level to the next by simply withholding instruction and information is not the best way to go about (even though I think it works ok in this case). As the “melting ice cubes” experiment shows unexpected results, it usually organically leads into open inquiry as people tend to start asking “what would happen if…?” questions, which I then encourage them to pursue (but this usually only happens in a second step, after they have already run the experiment “my way” first). This relates well to “secret objectives” (Bartlett and Dunnett, 2019), where a discrepancy appears between what students expect based on previous information and what they then observe in reality (for example in the “melting ice cube” case, students expect to observe one process and find out that another one dominates), and where many jumping-off points exist for further investigation, e.g. the condensation pattern on the cups, or the variation of parameters (what if the ice was forced to the bottom of the cup? what’s the influence of the exact temperatures or the water depth, …?).
Introducing an element of surprise might generally be a good idea to spark interest and inquiry. Huber & Moore (2001) suggest using “discrepant events” (their example is dropping raisins in carbonated drinks, where they first sink to the bottom and then raise as gas bubbles attach to them, only to sink again when the bubbles break upon reaching the surface) to initiate discussions. They then suggest following up the observation of the discrepant event with a “can you think of a way to …?” question (i.e. make the raisin raise faster to the surface). The “can you think of a way to…?” question is followed by brainstorming of many different ideas. Later, students are asked “can you find a way to make it happen?”, which then means that they pick one of their ideas and design and conduct an experiment. Huber & Moore (2001) then suggest a last step, in which students are asked to do a graphical representation or of their results or some other product, and “defend” it to their peers.
In contrast to how I run my favourite “melting ice cubes” experiment when I am instructing it in real time, I am using a lot of confirmation experiences, for example in my advent calendar “24 days of #KitchenOceanography”. How could they be re-imagined to lead to more investigation and less cook-book-style confirmation, especially when presented on a blog or social media? Ha, you would like to know, wouldn’t you? I’ve started working on that, but it’s not December yet, you will have to wait a little! :)
I’m also quite intrigued by the “product” that students are asked to produce after their experimentation, and by what would make a good type of product to ask for. In the recent iEarth teaching conversations, Torgny has been speaking of “tangible traces of learning” (in quotation marks which makes me think there is definitely more behind that term than I realize, but so far my brief literature search has been unsuccessful). But maybe that’s why I like blogging so much, because it makes me read articles all the way to the end, think a little more deeply about them, and put the thought into semi-cohesive words, thus giving me tangible proof of learning (that I can even google later to remind me what I thought at some point)? Then, maybe everybody should be allowed to find their own kind of product to produce, depending on what works best for them. On the other hand, for the iEarth teaching conversations, I really like the format of one page of text, maximum, because I really have to focus and edit it (not so much space for rambling on as on my blog, but a substantially higher time investment… ;-)). Also I think giving some kind of guidance is helpful, both to avoid students getting spoilt for choice, and to make sure they focus their time and energy on things that are helping the learning outcomes. Cutting videos for example might be a great skill to develop, but it might not be the one you want to develop in your course. Or maybe you do, or maybe the motivational effects of letting them choose are more important, in which case that’s great, too! One thing that we’ve done recently is to ask students to write blog or social media posts instead of classical lab reports and that worked out really well and seems to have motivated them a lot (check out Johanna Knauf’s brilliant comic!!!).
Kirsty also mentioned a second point regarding the Buck et al. (2008) rubric to keep in mind: it is just about what is provided by the teacher, not about the students’ role in all this. That’s an easy trap to fall into, and one that I don’t have any smart ideas about right now. And I am looking forward to discussing more thoughts on this, Kirsty :)
In any case, the rubric made me think about inquiry in labs in a new way, and that’s always a good thing! :)
—
Bartlett, P. A. and K. Dunnett (2019). Secret objectives: promoting inquiry and tackling preconceptions in teaching laboratories. arXiv:1905.07267v1 [physics.ed-ph]
Buck, L. B., Bretz, S. L., & Towns, M. H. (2008). Characterizing the level of inquiry in the undergraduate laboratory. Journal of college science teaching, 38(1), 52-58.
Huber, R.A., and C.J. Moore. 2001. A model for extending hands-on science to be inquiry based. School Science and Mathematics 101 (1): 32–41.
I am currently teaching a lot of workshops on higher education topics where participants (who previously didn’t know each other, or me) spend 1-1.5 days talking about topics that can feel emotional and intimate and where I want to create an environment that is open and full of trust, and where connections form that last beyond the time of the workshop and help participants build a supportive network. So a big challenge for me is to make sure that paticipants quickly feel comfortable with each other and me.
As I am not a big fan of introductory games and that sort of things, for a long time I just asked them to introduce themselves and mention the “one question they need answered at the end of the workshop to feel like their time was well invested” (way to put a lot of pressure on the instructor! But I really like that question and in any case, it’s better to know the answer than to be constantly guessing…).
For the last couple of workshops, I have added another question, and that is to ask participants to quickly introduce us to their “nerd topic”*, which we define as the topic that they like to spend their free time on, wish they could talk about at any time and with anyone, and that just makes them happy. For me, that’s obviously kitchen oceanography!
Introductions in my workshops usually work like this: I go first and introduce myself. I make sure to not talk about myself in more detail than I want them to talk about themselves and to not include a lot of orga info at this point so I am not building a hierarchy of me being the instructor who gets to talk all the time, and then them being the participants who only get to say a brief statement each when I call on them. I model the kind of introduction I am hoping for to make it clear what I am hoping for from them. Then I call on people in the order they appear on my zoom screen and they introduce themselves. (I hate the “everybody pass the word on to someone who hasn’t spoken yet!” thing because it’s hugely stressful to me and making sure I call on someone who really hasn’t spoken yet and don’t forget anyone binds all my mental capacities if I am a participant. So when I am the workshop lead, I do call people myself and check off a list who has spoken already).
Including the “nerd topic” question has worked really well for me. Firstly, I LOVE talking about kitchen oceanography, and getting to talk about it (albeit really briefly) in the beginning of a workshop (when I am usually a little stressed and flustered) makes me happy and relaxes me. My excitement for kitchen oceanography shows in the way I speak, and I get positive feedback from participants right away. Even if kitchen oceanography isn’t necessarily their cup of tea, they can relate to the fascination I feel for a specific topic that not many other people care for.
And the same happens when, one after the other, the other participants introduce themselves. Nerd topics can be anything, and in the recent workshops topics ranging from children’s books to reading about social justice, from handcrafts to gardening, from cooking beetroots with spices to taste like chocolate to fermenting all kinds of foods, from TV series to computer games, from pets to children, from dance to making music. People might not come forward with their nerdiest nerd topics or they might make them sound nerdier than they actually are (who knows?), but so far for every nerd topic, there have been nods and smiles and positive reactions in the group and it is very endearing to see people light up when they talk about their favorite things. Participants very quickly start referencing other people’s nerd topics and relating them to their own, and a feeling of shared interests (or at least shared nerdiness) and of community forms.
Since they fit so well with the content of my workshops, I like to come back to nerd topics throughout the workshops. When speaking about motivation, they are great to reflect on our own motivation (what makes you wanting to spend your Saturday afternoons and a lot of money on this specific topic?). When speaking about the importance of showing enthusiasm in teaching, they were a perfect demonstration of how people’s expressions changed from when they talked about their job title and affiliation to talking about their nerd topic. Also practicing designing intriguing questions is easier when the subject is something you are really passionate about. Nerd topics are also great as examples to discuss the difference between personal and private — sharing personal information, showing personality, is a great way to connect with other people, but it does not mean that we need to share private information, too. And if participants are thinking about their USP when networking online, connecting their field of study with their nerd topic always adds an interesting, personal, unique touch.
Maybe “nerd topics” are especially useful for the kind of workshops I teach and not universally the best icebreaker question. In any case, for my purposes they work super well! But no matter what the nature of the workshop: Self-disclosure has been shown to lead to social validation and formation of professional relationships, both in online professional communities (Kou & Gray, 2018) and in classrooms (Goldstein & Benassi, 1994) and other settings. Listening to others disclosing information about themselves makes people like the other party better. But there is some reciprociticy in this: openness fosters openness, and as soon as the roles are reversed, the second person disclosing information can catch up on being liked, and the more is disclosed from both sides, the more the liking and other positive emotions like closeness and enjoyment grow (Sprecher et al. 2013). So maybe asking about participants’ “nerd topics” is a good icebreaker question for your classes, too?
*While I really like the longer form of the question, I’m actually not super happy with the term “nerd topic” itself. But I don’t have a good and less charged alternative. If you have any suggestions, I’d love to hear them!
—
Goldstein, G. S., & Benassi, V. A. (1994). The relation between teacher self-disclosure and student classroom participation. Teaching of psychology, 21(4), 212-217.
Kou, Y., & Gray, C. M. (2018). ” What do you recommend a complete beginner like me to practice?” Professional Self-Disclosure in an Online Community. Proceedings of the ACM on Human-Computer Interaction, 2(CSCW), 1-24.
Sprecher, S., Treger, S., & Wondra, J. D. (2013). Effects of self-disclosure role on liking, closeness, and other impressions in get-acquainted interactions. Journal of Social and Personal Relationships, 30(4), 497-514.
Several things happened today.
Turns out that even though I really like seeing posts in this format on other people’s Instagram, it’s way too much of a hassle for me to do it regularly :-D
Also a nightmare in terms of accessibility without proper alt-text, and for google-ability of the blog post. So I won’t be doing this again any time soon! But I’m still glad I tried!
And also: check out the book!
Invisible Learning: The magic behind Dan Levy’s legendary Harvard statistics course. David Franklin (2020)
One of my pet peeves are student evaluations that are interpreted way beyond what they can actually tell us. It might be people not considering sample sizes when looking at statistics (“66,6% of students hated your class!”, “Yes, 2 out of 3 responses out of 20 students said something negative”), or not understanding that student responses to certain questions don’t tell us “objective truths” (“I learned much more from the instructor who let me just sit and listen rather than actively engaging me” (see here)). I blogged previously about a couple of articles on the subject of biases in student evaluations, which were then basically a collection of all the scary things I had read, but in no way a comprehensive overview. Therefore I was super excited when I came a sytematic review of the literature this morning. And let me tell you, looking at the literature systematically did not improve things!
In the article “Sexism, racism, prejudice, and bias: a literature review and synthesis of research surrounding student evaluations of courses and teaching.” (2021), Troy Heffernan reports on a systematic analysis of the existing literature of the last 30 years represented in the major databases, published in peer-reviewed English journals or books, and containing relevant terms like “student evaluations” in their titles, abstracts or keywords. This resulted in 136 publications being included in the study, plus an initial 47 that were found in the references of the other articles and deemed relevant.
The conclusion of the article is clear: Student evaluations of teaching are biased depending on who the students are that are evaluating, depending on the instructor’s person and prejudices that are related to characteristics they display, depending on the actual course being evaluated, and depending on many more factors not related to the instructor or what is going on in their class. Student evaluations of teaching are therefore not a tool that should be used to determine teaching quality, or to base hiring or promotion decisions on. Additionally, those groups that are already disadvantaged in their evaluation results because of personal characteristics that students are biased against, also receive abusive comments in student evaluations that are harmful to their mental health and wellbeing, which should be reason enough to change the system.
Here is a brief overview over what I consider the main points of the article:
According to the studies compiled in the article, your course is evaluated differently depending on who the students are that are evaluating it. Female students evaluate on average 2% more positively than male students. The average evaluation improves by up to 6% when given by international students, older students, external students or students with better grades.
It also depends on what course you are teaching: STEM courses are on average evaluated less positively than courses in the social sciences and humanities. And comparing quantitative and qualitative subjects, it turns out that subjects that have a right or wrong answer are also evaluated less positively than courses where the grades are more subjective, e.g. using essays for assessment.
Additionally, student evaluations of teaching depend on even more factors beside course content and effectiveness, for example class size and general campus-related things like how clean the university is, whether there are good food options available to students, what the room setup is like, how easy to use course websites and admission processes are.
Many studies show that gender, ethnicity, sexual identity, and other factors have a large influence on student evaluations of teaching.
Women (or instructors wrongly perceived as female, for example by a name or avatar) are rated more negatively than men and, no matter the factual basis, receive worse ratings at objective measures like turnaround time of essays. Also the way students react to their grades depends on their instructor’s gender: When students get the grades they expected, male instructors get rewarded with better scores, when their expectations are not met, men get punished less than women. The bias is so strong that for young (under 35 years old) women teaching in male-dominated subjects, this has been shown to have an effect of up to 37% lower ratings for women.
These biases in student evaluations result in strengthening the position of an already privileged group: white, able-bodied, heterosexual, men of a certain age (ca 35-50 years old), who the students believe to be heterosexual and who are teaching in their (and their students’) first language get evaluated a lot more favourable than anybody who does not meet one or several of the criteria.
Sometimes evaluations are also used by students to express anger or frustration, and this can lead to abusive comments. Those comments are not distributed equally between all instructors, though, they are a lot more likely to be directed at women and other minorities, and they are cummulative. The more minority characteristics an instructor shows, the more abusive comments they will receive. This racist, sexist, ageist, homophobic abuse is obviously hurtful and harmful to an already disadvantaged population.
Reading the article, I can’t say I was surprised by the findings — unfortunately my impression of the general literature landscape on the matter was only confirmed by this systematic analysis. However, I was positively surprised to read the very direct way in which problematic aspects are called out in many places: “For example, women receive abusive comments, and academics of colour receive abusive comments, thus, a woman of colour is more likely to receive abuse because of her gender and her skin colour“. This is really disheartening to read on the one hand because it becomes so tangible and real, especially since in addition to being harmful to instructors’ mental health and well-being when they contain abuse, student evaluations are also still an important tool in determining people’s careers via hiring and promotion decisions. But on the other hand it really drives home the message and call to action to change these practices, which I really appreciate very much: “These practices not only harm the sector’s women and most underrepresented and vulnerable, it cannot be denied that [student evaluations of teaching] also actively contribute to further marginalising the groups universities declare to protect and value in their workforces.”.
So let’s get going and change evaluation practices!
Heffernan, T. (2021). Sexism, racism, prejudice, and bias: a literature review and synthesis of research surrounding student evaluations of courses and teaching. Assessment & Evaluation in Higher Education, 1-11.
I’ve been leading a lot of workshops and doing consulting on university teaching lately, and one request that comes up over and over again is “just tell me what works!”. Here I am presenting an article that is probably the best place to start.
The famous “visible learning” study by Hattie (2009) compiled pretty much all available articles on teaching and learning, for a broad range of instructional settings. Their main conclusion was that the focus should be on visible learning, which means learning where learning goals are explicit, there is a lot of feedback happening between students and teachers throughout the interactions, and the learning process is an active and evolving endeavour, which both teachers and students reflect on and constantly try to improve.
However, what works at schools does not necessarily have to be the same that works at universities. Students are a highly select group of the general population, the ones that have been successful in the school system. For that group of people, is it still relevant what teaching methods are being used, or is the domain-specific expertise of the instructors combined with skilled students enough to enable learning?
The article “Variables associated with achievement in higher education: A systematic review of meta-analyses” by Schneider & Preckel (2017) systematically brings together what’s known about what works and what doesn’t work in university teaching, and their main findings.
Below, I am presenting the headings of the “ten cornerstone findings” as quotes from the article, but I am providing my own interpretations and thoughts based on their findings.
Even though instructors might not always be aware of it because literature on university teaching has been theoretical for a long time (or they just don’t have the time to read enough to gain an overview over the existing literature), but these days there is a lot of empirical evidence of what makes university teaching effective!
There is a HUGE body of literature on studies investigating what works and what does not, but results always depend on the exact context of the study: who taught whom where, using what methods, on what topic, … Individual studies can answer what worked in a very specific context, but they don’t usually allow for generalizations.
To help make results of studies more generally valid, scientists bring together all available studies on a particular teaching method, “type” of student or teacher in meta studies. By comparing studies in different context, they can identify success factors of applying that specific method across different contexts, thus making it easier to give more general recommendations of what methods to use, and how.
But then if you aren’t just interested in how to use one method, but what design principles you should be applying in general, you might want to look at systematic reviews of meta-studies. Systematic review of meta-studies bring together everything that has been published on a given topic and try to distill the essence from that. One such systematic review of meta-studies is the one I am presenting here, where the authors have compiled 38 meta-analyses (which were found to be all available meta-analyses relevant to higher education) and thus provide “a broad overview and a general orientation of the variables associated with achievement in higher education”.
A big challenge with investigations of teaching effectiveness is that most characteristics of teaching and of learners are related to achievement. So great care needs to be taken in order to not interpret the effect one measures for example in a SoTL project as the optimal effect, because some characteristics and their related effects are much larger than others: “The real question is not whether an instructional method has an effect on achievement but whether it has a higher effect size than alternative approaches.”
This is really important to consider especially for instructors who are (planning on) trying to measure how effective they or their methods are, or who are looking in the literature for hints on what might work for them — it’s not enough to just look if a method does have a positive effect, but to consider whether even more effective alternatives might exist.
Great news! What we do as teachers does influence how much students learn! And often times it is through really tiny things we do or don’t do, like asking open-ended questions instead of closed-ended ones, writing keywords instead of full sentences on our slides or the blackboard (for more examples, see point 5).
And there are general things within our influence as teachers that positively contribute to student learning, for example showing enthusiasm about the content we are teaching, being available to students and being helpful, and treating the students respectfully and friendly. All these behaviours help create an atmosphere in which students feel comfortable to speak their minds and interact, both with their teacher and among each others.
But it is, of course, also about what methods we chose. For example, choosing to have students work in small groups is on average more effective than having them learn both individually or as the whole group together. And small groups become most effective when students have clear responsibilities for tasks and when the group depends on all students’ inputs in order to solve the task. Cooperation and social interaction can only work when students are actively engaged, speak about their experiences, knowledge and ideas, discuss and evaluate arguments. This is what makes it so successful for learning.
It would be nice to know that just by using certain methods, we can increase teaching effectivity, but unfortunately they also need to be implemented in the right way. Methods can work better or not so well, depending on how they are done. For example, asking questions is not enough, we should be asking open instead of closed questions. So it is not only about using large methods, but to tweak the small moments to be conductive to learning (examples for how to do that under point 5)
Since microstructure (all the small details in teaching) is so important, it is not surprising that the more time teachers put into planning details of their courses, the higher student achievement becomes. Everything needs to be adapted to the context of each course: who the students are and what the content is. This is work!
So now that we know that teachers can increase how much students learn in their classes, here is a list of what works (and many of those points are small and easy to implement!)
Even though all these points are small and easy to implement, their combined effect can be large!
There was no meta-analysis directly comparing teacher-centered and student-centered teaching methods, but elements of both have high effects on student learning. The best solution is to use a combination of both, for example complementing teacher presentations by interactive elements, or having the teacher direct parts of student projects.
Social interaction is really important and maximally effective when teachers on the one hand take on the responsibility to explicitly prepare and guide activities and steer student interactions, while on the other hand giving students the space to think for themselves, choose their own paths and make their own experiences. This means that ideally we would integrate opportunities for interaction in more teacher-centered formats like lectures, as well as making sure that student-centered forms of learning (like small groups or project-based learning) are supervised and steered by the instructor.
We didn’t have a lot of choice in the recent rise of online learning, but the good news is that it can be pretty much as effective as in-person learning in the classroom. Blended learning, i.e. combining online and in-class instruction, is even more effective, especially when it is used purposefully for visualizations and such.
Blended learning is not as successful as in-person learning when used mainly to support communication; compared to in-person, online communication is limiting social interaction (or at least it was before everybody got used to it during covid-19? Also, the article points out explicitly that instructional technologies are developing quickly and that only studies were included that were published before 2014. Therefore MOOCs, clickers, social media and other newer technologies are not included).
Despite constructive alignment being one of the buzzwords that is everywhere these days, the focus of most instructors is still on the presentation part of their courses, and not equally on assessment. But the results presented in the article indicate that “assessment practices are related to achievement about as strongly as presentation practices”!
But assessment does not only mean developing exam questions. It also means being explicit about learning goals and what it would look like if they were met. Learning outcomes are so important! For the instructor to plan the whole course or a single class, to develop meaningful tests of learning and then actually evaluating it, in order to give feedback to students. Students, on the other hand, need guidance on what they should focus on both in reflecting on what they learned during past lessons, preparing for future lessons, and preparing for the exam.
Assessment also means giving formative feedback (feedback with the explicit and only purpose of helping students learn or teachers improve teaching, not giving a final evaluation after the fact) throughout the whole teaching process.
Assessment also doesn’t only mean the final exam, it can also mean smaller exercises or tasks throughout the course. Testing frequently (more than two or three times per semester) helps students learn more. Requiring that students show they’ve learnt what they were supposed to learn before the instructor moves on to the next topic has a large influence on learning. And the frequent feedback that can be provided on that basis helps them learn even more.
And: assessment can also mean student-peer assessment or student self-assessment, which agree on average fairly well with assessment by the instructor but have the added benefit of explicitly thinking about learning outcomes and whether they have been achieved. Of course, this is only possible when learning outcomes are made explicit.
The assessment part is so important, because students optimize where to spend their time based on what they perceive as important, which is often related to what they will need to be able to do in order to pass an exam. The explicit nature of the learning outcomes (and their alignment with the exam) are what students use to decide what to spend time and attention on.
Even though we as instructors have a large influence on student achievement by all the means described above, there are also student characteristics that influence how well students can achieve. Intelligence and prior achievement are correlated to how well pupils will do at university (although both are not fixed characteristics that students are born with, but formed by how much and what quality of education students attended up to that point). If we want better students, we need better schools.
Despite student backgrounds and personalities being important for student achievement, even more important are what strategies they are using to learn, to prepare for exams, to set goals and regulate how much effort they put on what task. Successful strategies are frequent class attendance as well as a strategic approach to learning, meaning that instead of working hard non stop, students allocate time and effort to those topics and problems that are most important. But also on the small scale, what students do matters: Note taking, for example, is a much more successful strategy when students are listening to a talk without slides. When slides are present, the back-and-forth between slides and notes seems to distract students from learning.
Training strategies works best in class rather than outside in extra courses with artificial problems.
There you have it, that was my summary of the Schneider & Preckel (2017) systematic review of meta-analyses of what works in higher education. We know now of many things that work pretty much universally, but even though many of the small practices are easy to implement, it still doesn’t tell us what methods to use for our specific class and topic. So where do we go from here? Here are a couple of points to consider:
Look for examples in your discipline! What works in your discipline might be published in literature that was either not yet used in meta-studies, or published in a meta-study after 2014 (and thus did not get included in this study). So a quick literature search might be very useful! In addition to published scientific studies, there is a wealth of information available online of what instructors perceive to be best practice (for example SERC’s Teach the Earth collection, blogs like this one, tweets collected under hashtags like #FieldWorkFix, #HigherEd). And of course always talk to people teaching the same course at a different institution or who taught it previously at yours!
Look for examples close to home! What works and what doesn’t is also culture dependent. Try to find out what works in similar courses at your institution or a neighboring one with the same or a similar student body and similar learning outcomes?
And last not least: Share your own experiences with colleagues! Via twitter, blogs, workshops, seminars. It’s always good to share experiences and discuss! And on that note — do you have any comments on this blog post? I’d love to hear from you! :)
Schneider, M., & Preckel, F. (2017). Variables associated with achievement in higher education: A systematic review of meta-analyses. Psychological bulletin, 143(6), 565.
Recently, one topic seemed to emerge a lot in conversations I’ve been having: Students cheating, or the fear thereof. Cheating is “easier” when exams are written online and we don’t have students directly under our noses, and to instructors it feels like cheating has increased a lot (and maybe it has!). We’ve discussed all kinds of ways to avoid cheating: Asking questions that have answers that cannot easily be googled (but caution — this tends to make things a lot more difficult than just asking for definitions!). Putting enough time pressure on students so they don’t have time to look up things they don’t know (NOT a fan of that!!!). Using many different exams in parallel where students get assigned exercises randomly so that they would at least have to make sure they are copying from someone trying to answer the same question. But one question that has been on my mind a lot is why do students cheat in the first place, and is there anything we can do as instructors to influence whether they will want to cheat?
I read the chapter “Why students cheat: an exploration of the motivators of student academic dishonesty in higher education” in the Handbook of Academic Integrity by Brimble (2016) and here are some of the points, all backed up by different studies (for references, check back to that chaper), that stood out to me:
Students are under an enormous pressure to succeed academically, yet at the same time they are real people with lives, families, responsibilities, possibly jobs, and more. Whether its because of financial considerations, expectations of parents or peers, or other reasons: Cheating might sometimes feel like it’s the only solution to survive and finish a course among competing priorities.
Since students are under such a pressure to succeed, it is important to them that the playingfield is level and others don’t get an unfair and undeserved advantage over them. If students feel like everybody else is cheating, they might feel like they have to cheat in order to keep up. Also if the workload is so high they feel like they cannot possibly manage in other ways or content is so difficult, they feel like cheating is their only way out.
Students also feel that cheating is a “victimless crime”, so no harm done, really. Especially helping other students, even if that counts in fact as cheating, isn’t perceived as doing anything wrong. Especially if courses feel irrelevant to their lives or if students don’t have a relationship with the instructor, it does not feel like they are doing anything wrong by cheating.
Also in other cases, students might not even be aware that they are cheating (for example if they are new at university, or studying in interdisciplinary programs where norms differ between programs, or in situations that are new to them (like for example in open-book online exams, where it isn’t clear what needs to be cited and what’s common knowledge?).
Students report the actions of their role models in their academic field, their instructors, are super important in forming an idea of what is right and acceptable. If instructors don’t notice that students cheat, or worse, don’t react to it by reporting and punishing such a behavior, this feels almost like encouragement to cheat more, both to the original cheater and to others who observe the situation. Students then rationalize cheating even when they know it’s wrong.
Cheating is also a repeat offense — and the more a student does it, the easier it gets.
So from reading all of that, what can we do as instructors to lower the motivation to cheat?
If students don’t know exactly what we define as cheating, they cannot be blamed if they accidentally cheat. It’s our job to help them understand what cheating means in our specific context. We can probably all be a little more explicit about what is acceptable and what is not, especially in situations where there is a grey area. Of course it’s not a fun topic, but we need to be explicit about rules and also what happens when rules aren’t adhered to.
Interestingly, apparently the more involved students are in campus culture, the more they want to protect the institution’s reputation and not cheat. So building a strong environment that includes e.g. regularly communicated honor codes that become part of the culture might be beneficial, as well as helping students identify with the course, the study program, the institution.
It’s not enjoyable, but if we notice any cheating, we need to prosecute it and punish it, even though that might come at high costs to us in terms of time, conflict, admin. The literature seems to be really clear on this one: If we let things slide a little, they become acceptable.
Ideally we would know what the rules and procedures are like at our institutions if we see something that we feel is cheating, and who the people are that can support us in dealing with the situation. If not, maybe now is a good time to figure this out.
Cheating is more likely to occur when there are no, or only weak, instructor-student relationships. Additionally, if students don’t feel engaged in a course, if they don’t receive enough guidance by the instructor, or if a course feels irrelevant or like they aren’t learning anything anyway, students are more likely to cheat. Similarly if a course feels too difficult or too time-consuming, if the workload is too high, or if they feel treated unfairly.
So the lesson here is to build strong relationships and make the courses both engaging and relevant to students. Making sure that the learning outcomes are relevant in the curriculum and for students’ professional development is, of course, always good advice, but in the light of making students want to learn and not have them feel like they just need to tick a box (and then do it by cheating because it really doesn’t matter one way or the other). Explaining what they will be able to do once they meet the learning outcomes (both in terms of what doors the degree opens, but also what they can practically do with the skills they learned) is another common — nevertheless now particularly useful — piece of advice. And then adjusting level of difficulty and workload to something that is managable for students — again, good advice in general and now in particular!
Of course, doing all those things is not a guarantee that students won’t cheat. But to me it feels like if I’ve paid attention to all this, I did what I could do, and that then it’s on them (which makes it easier to prosecute? Hopefully?).
What do you think? Any advice on how to deal with cheating, and especially how to prevent it?
Brimble, M. (2016). Why students cheat: an exploration of the motivators of student academic dishonesty in higher education. Handbook of academic integrity, 365.