Tag Archives: DryTheory2JucyReality

Tilting frontal surface under rotation / cylinder collapse

Leave a reply

Torge and I are planning to run the “tilting of a frontal surface under rotation / cylinder collapse” experiment as “remote kitchen oceanography” in his class on Thursday, so I’ve been practicing it today. It didn’t work out quite as well as it did when Pierre and I were running it in Bergen years ago, so if you are looking for my best movie of that experiment, you should go read the old blog post.

The idea is that a density front is set up by spinning up a tank in which a bottom-less cylinder contains a denser fluid, set up into a less dense fluid. Once the tank is spun up, the cylinder is removed, releasing the denser fluid into the less dense one. In contrast to the non-rotating case, where the dense water would sink to the bottom of the tank and form a layer underneath the less dense water, here the cylinder changes its shape to form a cone that retains its shape. The slope of the front is determined by both the rotation rate and the density contrast.

What I can show you today is what it looks like on my DIYnamics rotating table in my kitchen (and it’s pretty cool that all these different experiments can be run on such a simple setup, isn’t it?!). This is from two weeks ago:

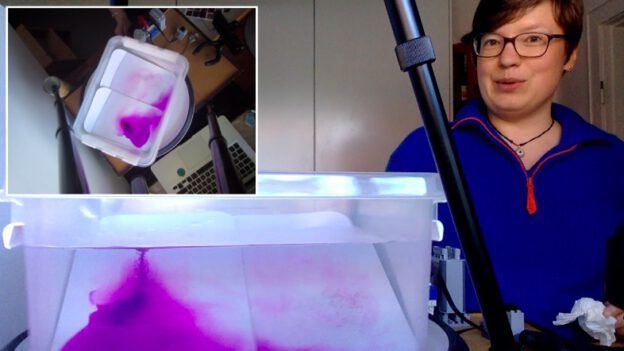
And a second attempt done today (I’m not showing you all the failed ones in between, and since I’m a little sick, I’m also not showing you what I look like, and spare you the sound of my incoherend explanations ;-)). But: Now everything is set up so I can use my right hand to pull out the cylinder to introduce fewer disturbances (spoiler alert: didn’t work out — see all the waves on the tank after I remove the cylinder?)

Check out the flower “floats” — the ones on the remains of the cylinder are rotating in the same direction as the tank, only faster! That’s something we didn’t show in Bergen and that I think is really neat.

What I learned about how to set up the experiment: I filled the cylinder with ice cubes and then filled water into the donut outside of the cylinder. That way, water pressure would push water through the petroleum jelly seal at the bottom of the cylinder inside, but the dye of the melting ice cubes would not seep out (very much). Also, the cold melt water would make the water inside the cylinder denser (make sure to stir!). The whole fancy “get water out and refill using a syringe” stuff sounds nice but just isn’t feasible in my setup…

In this case, having a larger tank would be really helpful, because the disturbances introduced in either case are probably more or less the same, but the smaller the tank, the larger the relative effect of a disturbance… Also, my tripod was making it really difficult for me to reach into the tank without hitting it, both for filling the tank and for removing the cylinder. I guess if we didn’t need a top view, things would be a lot easier… ;-)

Rotating vs non-rotating turbulence

3 Replies

Last Thursday, Torge & I invited his “atmosphere & ocean dynamics class” to a virtual excursion into my kitchen — to do some cool experiments. As you know, I have the DIYnamics rotating table setup at home, so this is what it looked like:

We did two experiments, the very boring (but very important) solid body rotation, and then the much more exciting (and quite pretty, see pic at the very top or movie below!) comparison of turbulence in a non-rotating and a rotating system.

We didn’t manage to record the class as we had planned, so I redid & recorded the experiments. Here are 8 minutes of me talking you through it. Enjoy!

A common misconception in rotating tank experiments, and one way of maybe not reinforcing it

3 Replies

A very common misconception when looking at atmosphere & ocean dynamics in a rotating tank is that the center of the tank represents one of the poles and the edge of the tank the equator. And there is one experiment that — I fear — might reinforce that misconception, and that is the one we love to show for rotation vs thermal forcing, baroclinic instabilities (fast
rotation), Hadley cell circulation (slow rotation).

When we do this experiment, the tank looks like a polar stereographic view of the Earth, with the pole (represented by the blue ice in the picture below) in the center and the equator at the edge of the tank. And when we then talk about the eddies we see as representing weather pattern, it’s all too easy to assume that the Coriolis parameter also varies throughout the tank similarly as it would on Earth, only projected down into the tank. Which is not the case!

But the good news is that it’s super easy to drive this experiment by heating rather than cooling in the center of the tank. The physics are exactly the same, only the heat transport is now happening radially outward rather than radially inward. And that it’s now not the easiest assumption any more that we are looking down at the pole.

Also: Heating in the middle is a lot easier to do spontaneously than cooling using ice — no overnight stay in the fridge required, just a kettle! :-)

What are other misconceptions related to rotating tanks that you commonly come across? And do you have any advice on how to prevent these misconceptions or elicit, confront, resolve them?

Solid body rotation

Leave a reply

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough that I’m

  1. Playing with it
  2. Making videos of me playing with it
  3. Putting the videos on the internet
  4. Going to do video calls with my friends’ classes, so that the students can at least “remote control” the hands-on experiments they were supposed to be doing themselves.

Here is me introducing the setup:

Today, I want to share a video I filmed the spinup of a tank until it reaches solid body rotation. To be clear: This is not a polished, stand-alone teaching video. It’s me rambling while playing. It’s supposed to give students an initial idea of an experiment we’ll be doing together during a video call, and that they’ll be discussing in much more depth in class. Watching a tank until it reaches olid body rotation is probably the most boding tank experiment ever done, but understanding the concept of solid body rotation and why we need it in tank experiments is the foundation of everything we do on a rotating tank. So here we go!

Thermal forcing vs rotation tank experiments in more detail than you ever wanted to know

Leave a reply

This is the long version of the two full “low latitude, laminar, tropical Hadley circulation” and “baroclinic instability, eddying, extra-tropical circulation” experiments. A much shorter version (that also includes the end cases “no rotation” and “no thermal forcing”) can be found here.

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough that I’m

  1. Playing with it
  2. Making videos of me playing with it
  3. Putting the videos on the internet
  4. Going to do video calls with my friends’ classes, so that the students can at least “remote control” the hands-on experiments they were supposed to be doing themselves.

Here is me introducing the setup:

Today, I want to share a video I filmed on thermal forcing vs rotation. To be clear: This is not a polished, stand-alone teaching video. It’s me rambling while playing. It’s supposed to give students an initial idea of an experiment we’ll be doing together during a video call, and that they’ll be discussing in much more depth in class. It’s also meant to prepare them for more “polished” videos, which are sometimes so polished that it’s hard to actually see what’s going on. If everything looks too perfect it almost looks unreal, know what I mean? Anyway, this is as authentic as it gets, me playing in my kitchen. Welcome! :-)

In the video, I am showing the two full experiments: For small rotations we get a low latitude, laminar, tropical Hadley circulation case. Spinning faster, we get a baroclinic instability, eddying, extra-tropical case. And as you’ll see, I didn’t know which circulation I was going to get beforehand, because I didn’t do the maths before running it. I like surprises, and luckily it worked out well!

Thermal forcing vs rotation

1 Reply

The first experiment we ever ran with our DIYnamics rotating tank was using a cold beer bottle in the center of a rotating tank full or lukewarm water. This experiment is really interesting because, depending on the rotation of the tank, it will display different regimes. For small rotations we get a low latitude, laminar, tropical Hadley circulation case. Spinning faster, we get a baroclinic instability, eddying, extra-tropical case. Both are really interesting, and in the movie below I am showing four experimentsm ranging from “thermal forcing, no rotation”, over two experiments which include both thermal forcing and rotation at different rates to show both the “Hadley cell” and “baroclinic instability” case, to “no thermal forcing, just rotation”. Enjoy!

Ekman layers in my kitchen

Leave a reply

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough that I’m

  1. Playing with it
  2. Making videos of me playing with it
  3. Putting the videos on the internet
  4. Going to do video calls with my friends’ classes, so that the students can at least “remote control” the hands-on experiments they were supposed to be doing themselves.

Here is me introducing the setup:

Today, I want to share a video I filmed on Ekman layers. To be clear: This is not a polished, stand-alone teaching video. It’s me rambling while playing. It’s supposed to give students an initial idea of an experiment we’ll be doing together during a video call, and that they’ll be discussing in much more depth in class. It’s also meant to prepare them for more “polished” videos, which are sometimes so polished that it’s hard to actually see what’s going on. If everything looks too perfect it almost looks unreal, know what I mean? Anyway, this is as authentic as it gets, me playing in my kitchen. Welcome! :-)

In the video, I am stopping a tank that was spun up into solid body rotation, to watch a bottom Ekman layer develop. Follow along for the whole journey:

Now. What are you curious about? What would you like to try? What would you do differently? Any questions for me? :-)

Rossby-#WaveWatchingWednesday

2 Replies

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough that I’m

  1. Playing with it
  2. Making videos of me playing with it
  3. Putting the videos on the internet
  4. Going to do video calls with my friends’ classes, so that the students can at least “remote control” the hands-on experiments they were supposed to be doing themselves.

Here is me introducing the setup:

Today, I want to share a video I filmed on planetary Rossby waves. To be clear: This is not a polished, stand-alone teaching video. It’s me rambling while playing. It’s supposed to give students an initial idea of an experiment we’ll be doing together during a video call, and that they’ll be discussing in much more depth in class. It’s also meant to prepare them for more “polished” videos, which are sometimes so polished that it’s hard to actually see what’s going on. If everything looks too perfect it almost looks artificial, know what I mean? Anyway, this is as authentic as it gets, me playing in my kitchen. Welcome! :-)

In the video, I am using an ice cube, melting on a sloping bottom in a rotating tank, to create planetary Rossby waves. Follow along with the whole process:

Also check out the video below that shows both a top- and side view of a planetary Rossby wave, both filmed with co-rotating cameras.

Previous blog posts with more movies for example here.

Now. What are you curious about? What would you like to try? What would you do differently? Any questions for me? :-)

A recent seminar presentation on “one should really play more!” and our rotating tanks

1 Reply

Using “One should really play more!” as title of a presentation in a serious scientific colloquium might seem like a bold move, but the gamble payed off: a large, interested audience including everyone from students to professors enthusiastically dropped ice cubes and food dye in our LEGO-driven rotating tanks and passionately discussed their observations when on Monday, Torge and I gave a presentation in the “Ocean Circulation and Climate Dynamics” colloquium at GEOMAR. After briefly presenting the context of our PerLe-funded “Dry Theory to Juicy Reality” project, we invited everybody to play, no wait … conduct experiments with four of our rotating tanks that we had set up. Nils, Ludwig, Jakob and Hendrik from our current atmosphere and ocean dynamics class were there to help out at each of the tanks to make sure that people actually dared to touch the equipment but also make sure that they would see something meaningful in each experiment, while David took amazing pictures (which you see over on our new teaching ocean sciences blog, these are all mine).

It was such a pleasure to see everybody — from students to retired professors — drop ice cubes and drip dye, falling to their knees to have a better angle to look at tanks, and enthusiastically discussing observations and theory. Even though I am convinced that everybody should really play more, it felt really good to see people enjoying it, and not only for the aspect of play, but also for the scientific discussions that are inevitably provoked when you look at tanks.

Also it was great to be back in that auditorium 10 years after having defended my PhD there. So many things have changed, yet so much remained the same!

Playing for #FlumeFriday

Leave a reply

Yesterday, we’ve had four rotating tables operating simultaneously, for three different experiments. The one that everybody is gathering around in the picture above is our favourite experiment: a slowly rotating tank with cooling in the middle that shows a nice 2D circulation instead of an overturning as we would expect in a non-rotating system.

A second group was doing an Ekman spiral experiment similar to this one.

If you are interested in observing the bottom boundary layer of a tank, it might look a bit weird to people who don’t know what you are up to…

And the other two experiments were the planetary Rossby wave experiments that I’ve written about so much before that it doesn’t really matter that I didn’t take any pictures this time round.