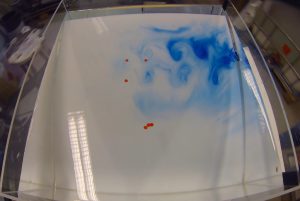
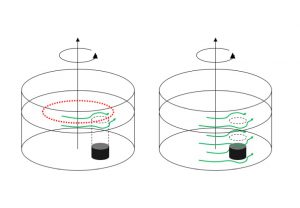
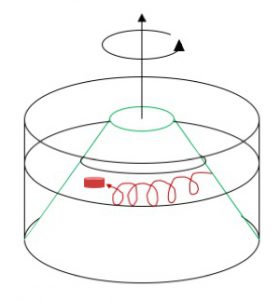
hand-on activity (difficult) Archives - Adventures in Oceanography and Teaching

Artikel “Praxisnähe dank digitaler Versuchsküche” von P. Mertsching über remote #KitchenOceanography

November 20, 2020

Im “eMagazin für aktuelle Themen der Hochschuldidaktik” der Uni Kiel ist der Artikel “Praxisnähe dank digitaler Versuchsküche” von Phil Mertsching über Torge’s und mein Projekt “Dry Theory 2 Juicy Reality”, insbesondere…

Collaborative Taylor column experiments during lockdown

November 12, 2020

We’ve become quite experienced with remotely-controlled rotating tank experiments, but the current lockdown brought us into yet another new-to-us situation: We had plans to film and live-stream tank experiments from…

Taylor column in rheoscopic fluid

October 12, 2020

I have a slightly complicated history with Taylor column experiments — even though the experiments look fine compared to all other videos I’ve found online, I somehow always had higher expectations.…

Tilting frontal surface under rotation / cylinder collapse

June 16, 2020

Torge and I are planning to run the “tilting of a frontal surface under rotation / cylinder collapse” experiment as “remote kitchen oceanography” in his class on Thursday, so I’ve…

A common misconception in rotating tank experiments, and one way of maybe not reinforcing it

June 5, 2020

A very common misconception when looking at atmosphere & ocean dynamics in a rotating tank is that the center of the tank represents one of the poles and the edge…

Solid body rotation

May 30, 2020

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough…

Rotating tank experiments on a cone

November 29, 2019

I had so much fun playing with rotating tank experiments on a cone this afternoon! And with Torge Martin (who I have the awesome #DryTheory2JuicyReality project with) and Rolf Käse…

Taylor column

October 16, 2019

I was super keen on trying the Taylor column experiment, but maybe I expected things to look too much like my sketch below, or my technique isn’t quite perfect yet,…

Topographic Rossby wave

September 29, 2019

Next attempt at the topographic Rossby wave! This time with following the geosci.uchicago.edu instructions more closely… …and then the tank had hickups, so we did get waves, but a lot more…

Planetary Rossby waves

September 28, 2019

I ran my new favourite experiment again, the planetary Rossby waves. They work super well on the DIYnamics table we built in Kiel and they also worked really well the other…

Planetary Rossby waves filmed with co-rotating camera

September 25, 2019

And here is my new favourite experiment again: Planetary Rossby waves! This time filmed with a co-rotating camera. We have a square tank with a sloping bottom at solid body…

Topographic Rossby wave

September 24, 2019

Finally trying the topographic Rossby wave experiment I wrote about theoretically here! And it is working — ok-ish. If you know what you are looking for, you can kind of…

Taylor column in a rotating tank

September 11, 2019

For both of my tank experiment projects, in Bergen and in Kiel, we want to develop a Taylor column demonstration. So here are my notes on the setup we are…

Rossby waves in a rotating tank — three different demonstrations

September 10, 2019

For both of my tank experiment projects, in Bergen and in Kiel, we want to develop a Rossby wave demonstration. So here are my notes on three setups we are…

Spin down — lots of shear instabilities in our tank!

August 30, 2019

When you stop a rotating tank, lots of stuff happens and it is usually very impressive to watch. Sometimes we stop tanks on purpose to show for example the development…

Parabolic surface shape of a tank of water in solid body rotation

August 29, 2019

One of the first exercises Torge and I plan on doing with the students in our “dry theory to juicy reality” project is to bring a water-filled tank to solid body…

Rotating vs non-rotating turbulence — now with movie!

August 27, 2019

Lots of demonstrations being prepared for Torge’s and my “dry theory to juicy reality” project. Shown here today: rotating vs non-rotating turbulence. Because the only way to really appreciate how…

Spinning dye curtain — when a tank full of water has not reached solid body rotation yet

August 26, 2019

With all the rotating tank experiments I’ve been showing lately, one thing that comes up over and over again is the issue of solid body rotation. On our DIYnamics-inspired turntable for…

Baroclinic instabilities / Hadley cell circulation in a tank

August 23, 2019

The DIYnamics-inspired turntable that Torge and myself have been working on for our “dry theory to juicy reality” project is finally working well! This is what the setup now looks…

Combining rotation of a water tank with a temperature gradient: A Hadley cell circulation demo!

August 15, 2019

Yesterday, we combined a thermally-driven overturning circulation with the effects of rotation, and thus created a Hadley cell circulation. And while the tank was turning faster than we would have…

Combining a slowly rotating water tank with a temperature gradient: A thermal wind demonstration!

August 14, 2019

Setting up an overturning circulation in a tank is easy, and also interpreting the observations is fairly straightforward. Just by introducing cooling on one side of a rectangular tank a…

Why do we need a rotating tank to study ocean and atmosphere dynamics? A demonstration

August 13, 2019

For our project “Ocean currents in a tank: From dry theory to juicy reality“, Torge, Joke and I are working on building affordable rotating tanks to use in Torge’s Bachelor…

Demonstrating Ekman layers in a rotating tank: High pressure and low pressure systems!

August 11, 2019

Ekman spirals — current profiles that rotate their direction over depth, caused by friction and Coriolis force — are really neat to observe in a rotating tank. I just found…

Working on our own affordable rotating table for oceanographic experiments!

July 6, 2019

Inspired by the article “Affordable Rotating Fluid Demonstrations for Geoscience Education: the DIYnamics Project” by the Hill et al. (2018), Joke, Torge and I have been wanting to build an affordable…

Supporting conceptual understanding of the Coriolis force through laboratory experiments

May 3, 2019

My friend Pierré and I started working on this article when both of us were still working at the Geophysical Institute in Bergen. It took forever to get published, mainly…

Tank demonstration of the circulation in a fjord

February 12, 2019

It has been a long time in the making, but finally we have a nice fjord circulation in our tank! Pierre and I tried to improve it 6 years ago,…

Lee waves with an asymmetrical “mountain”

October 25, 2018

How will lee waves look differently if we are using the asymmetrical mountain instead of the symmetric one? And is symmetry actually important at all or are we just looking…

Instructions: Dead water demonstration in the GFI basement

October 25, 2018

This blog post is meant as guidelines if someone other than me might have to set up this demonstration at some point… Have fun! :-) Setting up the stratification If…

Instructions: Lee wave demonstration in the GFI basement

October 24, 2018

This blog post is meant as guideline if someone other than me might have to set up this demonstration at some point… Have fun! :-) Lee waves Lee waves are…

Demonstration: Nansen’s “dead water” in a tank!

October 22, 2018

A ship that is continuously pulled with a constant force suddenly slows down, stops, and then continues sailing as if nothing ever happened? What’s going on there? We will investigate…

Accidental double-diffusive mixing

October 19, 2018

When setting up the stratification for the Nansen “dead water” demo (that we’ll show later today, and until then I am not allowed to share any videos, sorry!), I went…

The one where it would help to understand the theory better (but still: awesome tank experiment!)

August 16, 2018

The main reason why we went to all the trouble of setting up a quasi-continuous stratification to pull our mountain through instead of sticking to the 2 layer system we…

Fictitious forces (3/5): Coriolis force — how we think it should be taught

January 24, 2017

So how do we teach about the Coriolis force? The following is a shortened version of an article that Pierre de Wet and I wrote when I was still in…

Using the Monash Simple Climate Model as first exposure to “real” climate models

March 1, 2016

When talking to the “general public” (which sometimes just means friends or relatives) about working in climate sciences, it is sometimes really difficult to explain what it is we do…

Visualizing flow around a paddle

July 3, 2015

Whenever I’m in a canoe or kayak, I love watching the two eddies that form behind the paddle when you pull it through the water. It looks kinda like this:…

Wave fields around objects in a channel

February 25, 2015

One of the reasons I have been wanting to do the vortex street experiment I wrote about on Monday is that it is pretty difficult to visualize flow fields (especially if…

Salt fingering

August 28, 2014

My absolute favorite experiment ever: salt fingering. I know I’ve said it before about another experiment, even today, but this is my absolute favorite experiment and I still get endlessly…

Hydraulic jump II

March 17, 2014

More movies of my kitchen sink. I am really fascinated by the hydraulic jumps in my kitchen sink. I can’t believe I haven’t used this before when I was teaching!…

Hydraulic jumps

March 12, 2014

Water changing its velocity from above to below the critical velocity. Recently in beautiful Wetzlar: The river Lahn flows through the city below the medieval cathedral at sunset. And I’m…

Hydrostatic pressure

January 29, 2014

What are students not understanding about hydrostatic pressure? Tomorrow (today by the time this post will go online, I guess) I will present the paper “Identifying and addressing student difficulties…

Rogue waves in a bath tub

November 29, 2013

Trying to create rogue waves in the bath tub of the infamous “red house”. As a part of their projects, students in the CMM31 in Isafjördur course had to conduct…

Velocity of shallow water waves.

November 15, 2013

The experiment we run to discuss the velocity of shallow water waves. In this post, I discussed how it took us several years to modify an experiment to make it…

Seesawing of standing waves.

November 13, 2013

Improving one of the experiments run in the GEOF130 lab. One experiment that has been run in GEOF130 forever is the “standing wave”, where a wave is excited in a…

Fjord circulation

November 1, 2013

Tank experiment on a typical circulation in a fjord. Traditionally, a fjord circulation experiment has been done in GEOF130’s student practicals. Pierre and I recently met up to test-run the…

Measuring salinity

September 27, 2013

Students evaporate water to measure the salinity of a water sample. As described in this post, I like to have students build “instruments” to measure the most oceanographic properties (temperature, salinity…

Heat capacity of air and water

August 28, 2013

Hands-on activity to better understand the concept and consequences of heat capacity. Also a great party trick. Imagine you take a balloon. Any kind of normal balloon. You blow it…

How to measure temperature, salinity and density

August 28, 2013

Three in-class experiments run in parallel. Great if you want to discuss how properties are measured and what kind of difficulties you might encounter. Temperature, salinity and density are the…

Category: hand-on activity (difficult)

Contact me!

Subscribe to Blog via Email

Search "Adventures in Teaching and Oceanography"

Archives

Recent Posts

Categories

Tags