Taylor column
I was super keen on trying the Taylor column experiment, but maybe I expected things to look too much like my sketch below, or my technique isn’t quite perfect yet, but in any case, the results don’t look as good as I had hoped.
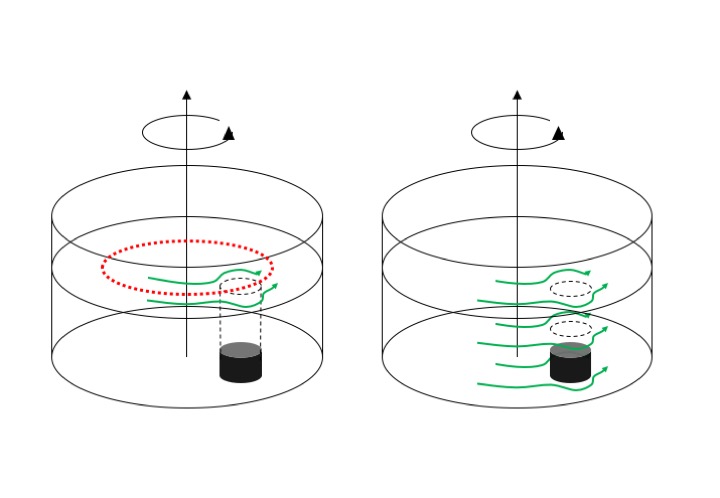
This is the setup I was aiming for:
- put ice hockey puck (two in our case), ca 1/5th water depth, ca 1/4 diameter of tank
- rotating our tank at 5rpm (ca 7 on GFI’s large tank’s display) with the obstacle in the water until solid body rotation is reached (We know that solid body rotation is reached if paper bits distributed on surface all rotate at same rate as the tank).
- change the rotation rate a tiny little bit so water moves relative to tank and obstacle, i.e. we have created a current flowing in the rotating system.
And here is what happened.
First attempt.
- tank was rotating way too fast
- tank wasn’t in solid body rotation because it wasn’t level
- one of the hockey pucks didn’t stay in place but moved to the edge of the tank as the tank (slowly!) accelerated
- more confetti on the surface!
But! We see that there is clearly something happening around the hockey puck that seems to deform the curtain of blue dye.
Second attempt.
- Stopped too rapidly / bumpy
Even though the blue dye curtain moves over the pucks initially, we see that they develop a wake or something, deforming the dye.
Third attempt.
Accidentally deleted the movie, so we will have to make do with a couple of pics I took while the experiment was running.
Slowing down worked a lot better this time round. We clearly see that the dye curtains are deformed around the Taylor columns and don’t move over the pucks.
Fourth attempt.
I think I am finally accepting that this way of introducing dye as a tracer isn’t working as I had hoped…
And this is when my camera decided to stop working…
Fifth attempt.
Back to the basics: Confetti floating on the surface.
Before slowing down, the field of confetti looked like this.
Then, the tank was slowed down and the field got deformed. Some confetti went over the puck, but there is an eddy downstream of it that catches confetti.
And the confetti that went over the puck seem to be stuck there.
Final attempt (for now).
More confetti. This is the situation before slowing down the tank:
Confetti distribution is influenced by the puck similarly to what we saw in the dye: Some confetti are slowed down upstream, some move around the puck.
Eventually, most confetti end up in the puck’s wake.
Barry Klinger says:
In the videos your Rossby number doesn’t look that small. I do the experiment using paper on the surface, and its tricky getting your flow to be slow enough for a small Rossby number but fast enough for the motion of the paper pellets not to be dominated by the surface tension effects that make them clump.
Another thing I noticed, last time I did this experiment, was that having a very black obstacle on a very white background makes it hard to visualize the taylor column, since whatever tracer shows up well over one color doesn’t over the other.
Taylor column in rheoscopic fluid - Adventures in Oceanography and Teaching says:
[…] have a slightly complicated history with Taylor column experiments — even though the experiments look fine compared to all other videos I’ve found […]
A Taylor column experiment that is kinda working – Elin Darelius & Team says:
[…] I haven’t given up on this! Here are a couple more attempts at Taylor columns in a tank under slightly different conditions. And if you have any suggestions, I’d love to hear them! […]