Category Archives: demonstration (difficult)

[annotated photo] Photo of water flowing over a weir, annotated with arrows showing particle velocities

Testing the new particle tracking app “Flow on the Go”

Leave a reply

The new particle tracking app “Flow on the Go” became available for testing on iOS yesterday. And it is SO AWESOME!!!

The idea is that particle that are advected in a flow can be used to visualize a flow field (similar to what we did when we were at the 13-m-diameter rotating swimming pool in Grenoble, where we added particles with neutral density to the tank in order to track currents). So the app latches on to something that it recognized as “particle” and then displays arrows as it follows that feature from frame to frame. Pretty amazing, isn’t it?

(If you are impatient, scroll to the second-to-last video of this post for my best example, otherwise stay with me as I walk you through different scenarios…)

First, I tested with movies I already had on my phone, for example storm waves in Kiel. Which might not be the nicest test case as wave crests break and thus new “particles” appear, but then vanish in a trough behind another wave etc.. So even though the app tracks them, it all seems a bit messy. The movies always start with a short glimpse of the original movie and then the tracking begins…

 

Then, I tried the “soap protects you from Corona” demo that my adorable nieces are presenting for you. There is water on the plate sprinkled with pepper (or something), and they dip their fingers in with a little bit of dish soap, break the surface tension, and the particles all get pushed to the edge of the plate. (Spoiler alert: Kids’ hands — no matter how cute — will be recognized as particles…. :-D)

 

At this point I decided that it was definitely time for my parents and me to go for a walk to film some flows.

Below: Laminar flow towards the edge, then turbulent flow at the bottom. Interesting observations here (beside the super cool flow field that is captured surprisingly well): Where there is a lot of foam and everything appears white, it’s not easy for the app to find “particles” to trace. And when reflections on the water move (like the handrail when there are waves) that looks like “particles” to the app.

 

Here is one example where there are plenty of bubbles passing by on the other side of the river (which are tracked very nicely) and my dad threw in some leaves on our side so there were particles that showed the recirculation. Nice! (No idea what the app sees in the top left corner, though)

 

Then I had the brilliant idea to film the large scale flow field with lots of bubbles in it. But, as you, dear reader, will probably have guessed already, the reflected trees are the much more dominant signal. That’s what happens when you film tons of things and only process them afterwards…

 

But here is a very nice example for you: Fast, laminar flow upstream of the weir, then a waterfall, a submerged hydraulic jump and turbulence at the bottom. Nice!

 

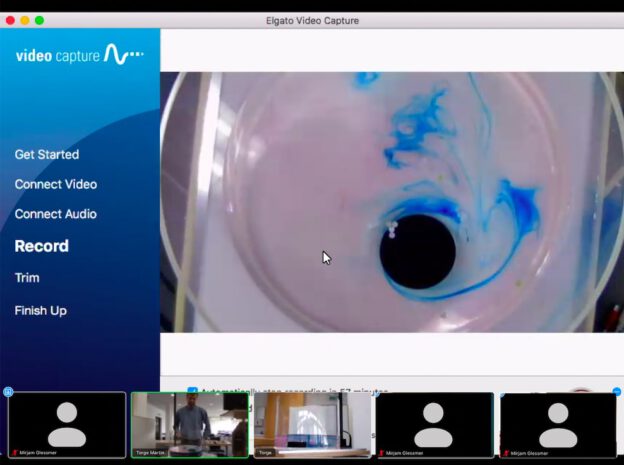
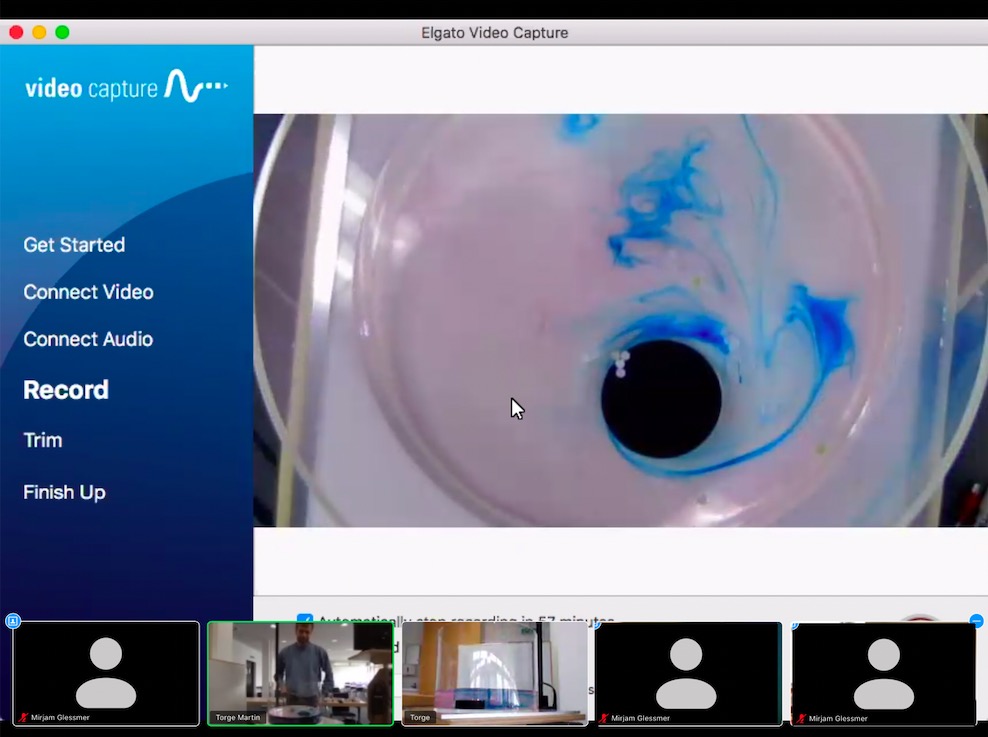
Back home, I decided I wanted to test some tank experiments. Below I’m first showing a couple of seconds of the original “thermal overturning circulation” movie (because I knew my hands would mess up the particle tracking when I’m dripping dye into the tank) and then cut to the processed one.

I thought that this was one of my better movies with few reflections on the tank, a nice background, etc.. Turns out: Still waaaay too much going on! Reflections on the glass, shadows on the wall behind it as we are watching… I’m sure there are settings in the app that would lead to much better results (if I knew how to use it) but for now I know that using the app is a little more difficult than I thought.

 

In any case, I think it’s a brilliant app, and I am looking forward to playing with it some more and figuring out how to use it best! There are so many settings that I haven’t figured out yet, so I know what I’ll be doing over the next couple of days… ;-) And I can’t wait to use it on our DIYnamics rotating tank experiments!

Artikel “Praxisnähe dank digitaler Versuchsküche” von P. Mertsching über remote #KitchenOceanography

Leave a reply

Im “eMagazin für aktuelle Themen der Hochschuldidaktik” der Uni Kiel ist der Artikel “Praxisnähe dank digitaler Versuchsküche” von Phil Mertsching über Torge’s und mein Projekt “Dry Theory 2 Juicy Reality”, insbesondere die Umsetzung im letzten Jahr mit den Zoom-Konferenzen aus meiner Küche, erschienen, zusammen mit vielen anderen spannenden virtuellen und hybriden Formaten. Es lohnt sich, da mal rein zu gucken!

Collaborative Taylor column experiments during lockdown

Leave a reply

We’ve become quite experienced with remotely-controlled rotating tank experiments, but the current lockdown brought us into yet another new-to-us situation: We had plans to film and live-stream tank experiments from Geomar, but not being employed there, I am currently not allowed in the building! So what happened this morning is that Torge and I met up on Zoom and I watched from home as he had all the fun.

It all started out quite well — camera tests worked well, water was in the tank, I was having fun taking screenshots. Well, and I was wishing I was there, playing, rather than watching and occassionally interrupting with instructions or unsolicited advice!

When we were done setting things up, students joined in for their exercise session (no, it’s not me three times in the meeting below, I just edited that in for privacy because we didn’t ask students for permissions to use their pictures), and a lively discussion ensued. Topic of the day were eddies in the ocean, and it was all leading up to the Taylor column experiment that we had only recently figured out.

The Taylor column experiment basically shows that rotating flows cannot just flow across an obstacle, they have to stay 2D and thus move around it. Which worked out beautifully! The blue dye started out upstream of the obstacle and got deformed into these beautiful filaments as it is moving around the hockey puck and the Taylor column on top of it (The puck is only blocking the lower part of the water column, above it there is just water!).

It all went super well until we fell into the trap we’ve been falling in ever since we started working with the tank: The co-rotating camera switches off when the power to the rotating table is switched off, which is the easiest way for the rotation to be switched off. So yeah. Below you see Torge trying to save the day by holding his laptop above the tank to give students a look into the tank after it stopped. Oh well…

But all in all, it worked super well and it’s great to see how virtual teaching and learning can be a really good substitute for in-person classes. But we are still looking forward to the times when we can all play together again!

Taylor column in rheoscopic fluid

Leave a reply

I have a slightly complicated history with Taylor column experiments — even though the experiments look fine compared to all other videos I’ve found online, I somehow always had higher expectations.

But now I’ve tried doing the experiment in a rheoscopic fluid (approximately 2cm of it over the hockey puck) and it looks a whole lot better in person than in these pics!

Here is a movie of the experiment. The Taylor column is created by first spinning up the tank to (almost, or in my case not quite because I didn’t have enough time but really wanted to try this) solid body rotation, and then slightly reducing the rotation rate (and then slightly increasing it again) in order to create a flow relative to the obstacle.

In the movie it becomes quite clear that while in the very beginning a lot of fluid gets advected across the puck, this does not happen when the fluid is (close to) solid body rotation. Then, there is a column of fluid (the Taylor column) spinning on top of the obstacle.

But there are other cool features visible in the movie, like the shear instabilities around the puck, and the lee waves downstream of it.

Can’t wait to spin this up to full solid body rotation on Thursday and try again!

Tilting frontal surface under rotation / cylinder collapse

Leave a reply

Torge and I are planning to run the “tilting of a frontal surface under rotation / cylinder collapse” experiment as “remote kitchen oceanography” in his class on Thursday, so I’ve been practicing it today. It didn’t work out quite as well as it did when Pierre and I were running it in Bergen years ago, so if you are looking for my best movie of that experiment, you should go read the old blog post.

The idea is that a density front is set up by spinning up a tank in which a bottom-less cylinder contains a denser fluid, set up into a less dense fluid. Once the tank is spun up, the cylinder is removed, releasing the denser fluid into the less dense one. In contrast to the non-rotating case, where the dense water would sink to the bottom of the tank and form a layer underneath the less dense water, here the cylinder changes its shape to form a cone that retains its shape. The slope of the front is determined by both the rotation rate and the density contrast.

What I can show you today is what it looks like on my DIYnamics rotating table in my kitchen (and it’s pretty cool that all these different experiments can be run on such a simple setup, isn’t it?!). This is from two weeks ago:

And a second attempt done today (I’m not showing you all the failed ones in between, and since I’m a little sick, I’m also not showing you what I look like, and spare you the sound of my incoherend explanations ;-)). But: Now everything is set up so I can use my right hand to pull out the cylinder to introduce fewer disturbances (spoiler alert: didn’t work out — see all the waves on the tank after I remove the cylinder?)

Check out the flower “floats” — the ones on the remains of the cylinder are rotating in the same direction as the tank, only faster! That’s something we didn’t show in Bergen and that I think is really neat.

What I learned about how to set up the experiment: I filled the cylinder with ice cubes and then filled water into the donut outside of the cylinder. That way, water pressure would push water through the petroleum jelly seal at the bottom of the cylinder inside, but the dye of the melting ice cubes would not seep out (very much). Also, the cold melt water would make the water inside the cylinder denser (make sure to stir!). The whole fancy “get water out and refill using a syringe” stuff sounds nice but just isn’t feasible in my setup…

In this case, having a larger tank would be really helpful, because the disturbances introduced in either case are probably more or less the same, but the smaller the tank, the larger the relative effect of a disturbance… Also, my tripod was making it really difficult for me to reach into the tank without hitting it, both for filling the tank and for removing the cylinder. I guess if we didn’t need a top view, things would be a lot easier… ;-)

A common misconception in rotating tank experiments, and one way of maybe not reinforcing it

3 Replies

A very common misconception when looking at atmosphere & ocean dynamics in a rotating tank is that the center of the tank represents one of the poles and the edge of the tank the equator. And there is one experiment that — I fear — might reinforce that misconception, and that is the one we love to show for rotation vs thermal forcing, baroclinic instabilities (fast
rotation), Hadley cell circulation (slow rotation).

When we do this experiment, the tank looks like a polar stereographic view of the Earth, with the pole (represented by the blue ice in the picture below) in the center and the equator at the edge of the tank. And when we then talk about the eddies we see as representing weather pattern, it’s all too easy to assume that the Coriolis parameter also varies throughout the tank similarly as it would on Earth, only projected down into the tank. Which is not the case!

But the good news is that it’s super easy to drive this experiment by heating rather than cooling in the center of the tank. The physics are exactly the same, only the heat transport is now happening radially outward rather than radially inward. And that it’s now not the easiest assumption any more that we are looking down at the pole.

Also: Heating in the middle is a lot easier to do spontaneously than cooling using ice — no overnight stay in the fridge required, just a kettle! :-)

What are other misconceptions related to rotating tanks that you commonly come across? And do you have any advice on how to prevent these misconceptions or elicit, confront, resolve them?

Solid body rotation

Leave a reply

Several of my friends were planning on teaching with DIYnamics rotating tables right now. Unfortunately, that’s currently impossible. Fortunately, though, I have one at home and enjoy playing with it enough that I’m

  1. Playing with it
  2. Making videos of me playing with it
  3. Putting the videos on the internet
  4. Going to do video calls with my friends’ classes, so that the students can at least “remote control” the hands-on experiments they were supposed to be doing themselves.

Here is me introducing the setup:

Today, I want to share a video I filmed the spinup of a tank until it reaches solid body rotation. To be clear: This is not a polished, stand-alone teaching video. It’s me rambling while playing. It’s supposed to give students an initial idea of an experiment we’ll be doing together during a video call, and that they’ll be discussing in much more depth in class. Watching a tank until it reaches olid body rotation is probably the most boding tank experiment ever done, but understanding the concept of solid body rotation and why we need it in tank experiments is the foundation of everything we do on a rotating tank. So here we go!

New rotating table on #FlumeFriday! Welcome to the family!

Leave a reply

In addition to our four DIYnamics-inspired rotating tanks, we now have a highly professional rotating table with SO MANY options! And also so much unboxing and constructing and trouble-shooting to do before it works. But we finished the first successful test: wanna see some rotating coffee in which milk is added? Then check this out!

Luckily Torge is patient enough to deal with me bossing him around, but it took forever to get the whole thing to work and I wanted my movie ;-)

Before we got to that point, though, did I mention that we had a lot of unboxing and constructing to do? But it was a bit like Christmas… And I can’t wait to play with every last piece of equipment! So many new and fun options for experiments I’ve always been wanting to do!

Happy #FlumeFriday! :-)

Rotating tank experiments on a cone

Leave a reply

I had so much fun playing with rotating tank experiments on a cone this afternoon! And with Torge Martin (who I have the awesome #DryTheory2JuicyReality project with) and Rolf Käse (who got me into tank experiments with an amazing lab course back in 2004, that I still fondly remember). We tried so many different things, that I will at some point have to describe in detail, but for now I just need to share the excitement ;-)

Here, for example, a blue fish-shaped ice cube. This experiment is pretty much the topographic Rossby wave experiment described here, except now we aren’t on an inclined plane, but on a cone. Which is basically an infinitely long inclined plane — the ice cube doesn’t encounter a boundary as it travels west, it just goes round and round the tank until it melts. And look at the cool Rossby waves!

Then we did another one of our favourite experiments, the Hadley cell circulation. What was really fascinating to observe was how turbulence the turbulence that was introduced by dripping dye into the tank changed scales. At first, we had the typical 3D pattern with plumes shooting down. But over time, the pattern became more and more organized, larger, and 2D. See below: The blue dye had been in the tank for a little longer than the red dye, so the structures look completely different. But interesting to keep that in mind when interpreting structures we observe!

Here is another view of the same experiment. Since we are cooling in the middle and rotating very slowly (about 3 rotations per minute), the eddy structures aren’t completely 2D, but they are influenced by an overturning component.

This looks even cooler when done on a cone. Can you see how there is both an overturning component (i.e. the plumes running down the slope) and then still a strong column in the middle?

This just looks so incredibly beautiful!

And one last look on the eddies that develop. We saw that there are cyclonic eddies happening in the center of the tank and anti-cyclonic eddies at the edge. Since we are on a cone, I could imagine that it’s just due to conservation of vorticity. Stuff that develops near the center and moves down the slope needs to spin cyclonically since the columns are being stretched, and on the other hand things that develop near the edge must move up the slope, thus columns being compressed. What do you think? What would be your explanation?

Nansen’s dead water explained on YouTube

Leave a reply

Remember the experiment on Nansen’s observation of “dead water” that Elin & myself set up as part of GEOF213? Our movies of this experiment are now featured in a brilliant Youtube video by my friend, the german science communicator Doktor Wissenschaft! Check it out! (English subtitles available)

I feel so proud to have contributed to such a cool video! :-)

 

P.S.: Doktor Wissenschaft also has an Instagram profile which is totally worth checking out. He posts interesting physics, chemistry and biology facts in twice daily. And occasionally he includes cool ocean and climate facts, supplied by yours truly. If you have fascinating facts that should be featured on Doktor Wissenschaft, please feel free to let me know and I will happily forward them!

One of Doktor Wissenschaft’s facts on Instagram: “If all Antarctic ice did melt, sea level would rise by approximately 58 meters”