Usually when we talk about waves on this blog, we talk about surface- or sometimes internal waves, but my waves almost always oscillate vertically. Today, we’ll mix things up a little: Rossby waves are waves in the horizontal plane. They exist for example as oscillations on the atmosphere’s jet stream. In order to understand what causes them, we need the concept of vorticity, which I will go over first before giving examples for Rossby waves.
Vorticity
Vorticity is a measure of how much a fluid is rotating. Generally speaking, once a fluid is in rotation, it wants to keep rotating (as we saw for example with the bottom Ekman layers in a rotating tank, where the water inside kept on rotating after the tank was stopped, until it was slowed down by friction). There are several components that are at play here — the rotation that we see when looking at eddies, the rotation of the Earth, and others — which I will go over in the following.
Relative vorticity
The easiest way to imagine what “vorticity” is (and the only one that I’ve talked about on this blog, see here), is to think of a little float in a flow. In a vorticity-free flow, that little float will always keep its orientation (see below). However if there is shear in the flow, i.e. the flow field carries vorticity, it will start to turn.
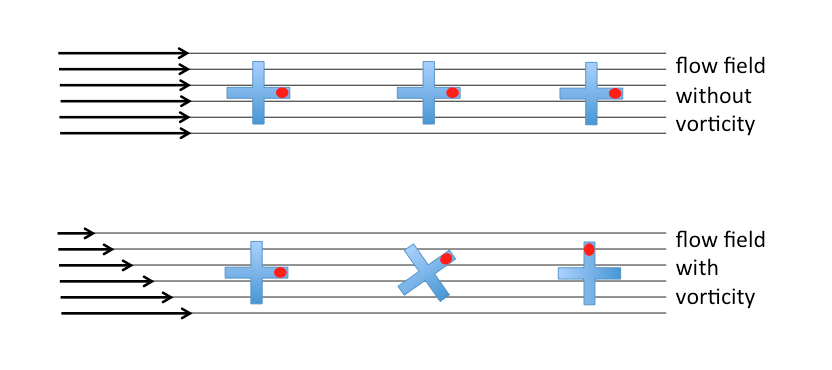
Flow fields without vorticity (top) and with vorticity (bottom).
Relative vorticity is what we see for example when looking al leaves swirling in rivers.
Planetary vorticity
Since the Earth is turning (and all the water on it with it), the water also carries planetary vorticity, i.e. the rotation of the Earth, which is the Coriolis parameter. The Coriolis parameter is largest at the poles and zero at the equator, meaning the rotation changes with latitude.
The rotation of the Earth is clearly important enough for us to want to spin our tanks to simulate its effects on ocean currents.
Absolute vorticity
The sum of relative and planetary vorticity is called absolute vorticity: This is how much any fluid column is rotating in total, including all possible components of rotation (which are only the two mentioned above, but still…).
Potential vorticity
One more factor that can influence the rotation of a fluid parcel is the water depth. When water depth increases, columns of water get expanded vertically (since, for continuity reasons, they still have to go all the way from surface to bottom, even if the distance is now larger) or, if water depth decreases, squished. Similarly to figure skaters that stretch or crouch to increase or decrease their rotation, the expansion of a column of water leads to a change in its rotation.
Potential vorticity is defined as absolute vorticity over water depth.
Conservation of potential vorticity leads to waves
Potential vorticity is conserved, so if water depth, planetary vorticity changes or relative vorticity changes, something else has to change to compensate. And if water changes how much it is rotating, this leads to meanders in currents, i.e. waves.
Depth is constant, but latitude changes: Planetary Rossby waves
Planetary vorticity changes with latitude, therefore if a water parcel moves in north-south direction over constant water depth, its relative vorticity needs to change in order for potential vorticity to be conserved. This leads to so-called planetary Rossby waves, where currents in the ocean or the atmosphere start oscillating in north-south direction (see figure below).
At position 1, a fluid parcel gets for any random reason pushed northward. As it moves north, its planetary vorticity increases and its relative vorticity therefore has to decrease to compensate (2). This leads to southward movement, but the initial latitude (3) is overshot a little (4). This again leads to a change in relative vorticity (4), which brings the water parcel back to its initial latitude (5), but it overshoots again… So this mechanism leads to a wave-like motion in the horizontal plane, with the phase of the wave propagating westward.
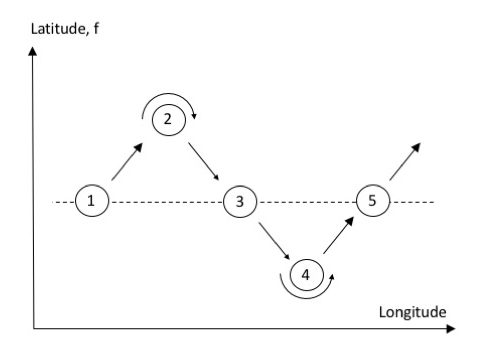
This can happen at any latitude, even at the equator where “equatorial planetary Rossby waves” occur. At the equator f=0, but as soon as the water column has moved slightly north or south from the equator, f kicks in and drives the water column back to the equator (where it then overshoots, is turned back, overshoots again…….).
Latitude is constant but depth changes: Topographic waves
If a current encountered a ridge, the water depth changes and the current thus gets deflected. This motion is called topographic wave: When a water column gets stretched, it gains relative vorticity, making it rotate cyclonically. When it runs into shallower water, it loses relative vorticity and starts turning the other way.
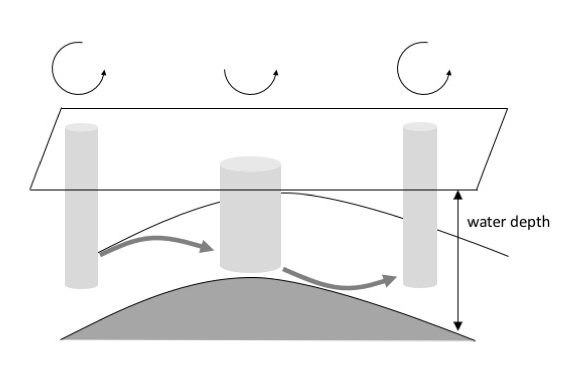
I’m hoping to set up demonstrations for both types of Rossby waves soon. Stay tuned! :-)


















