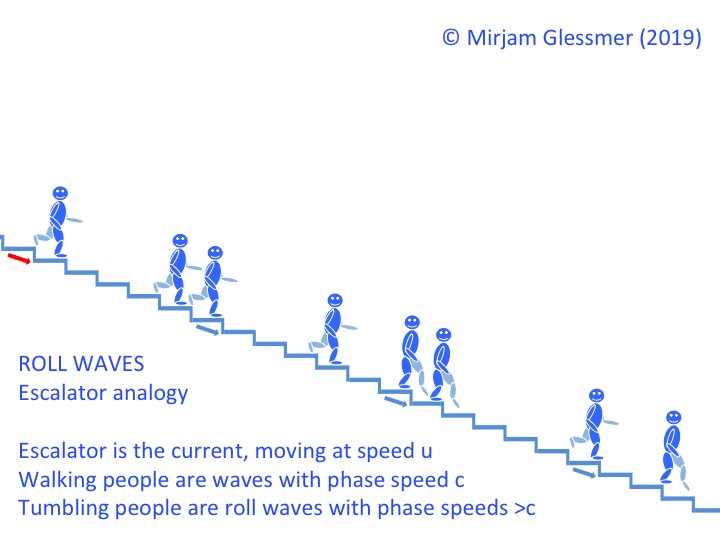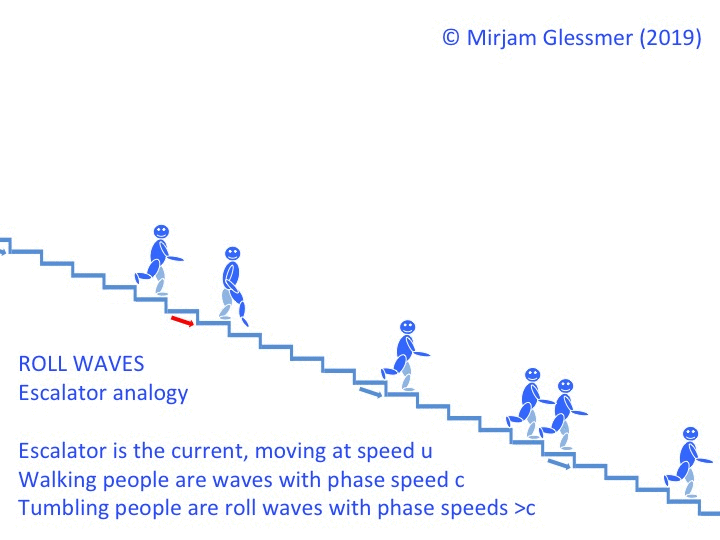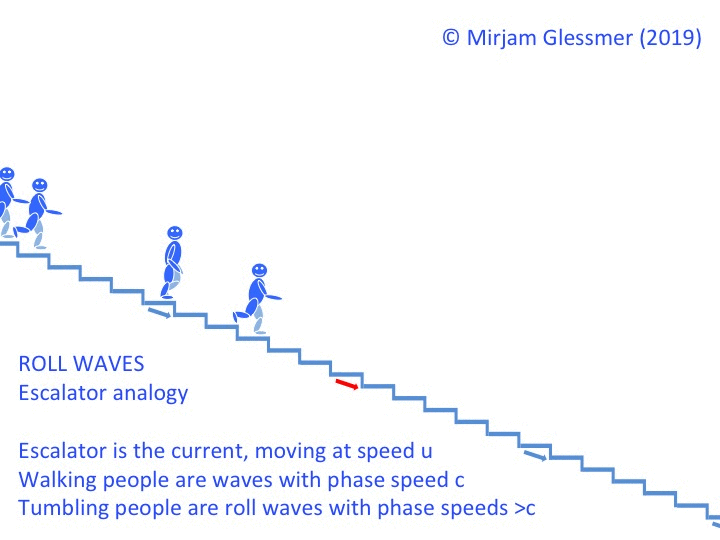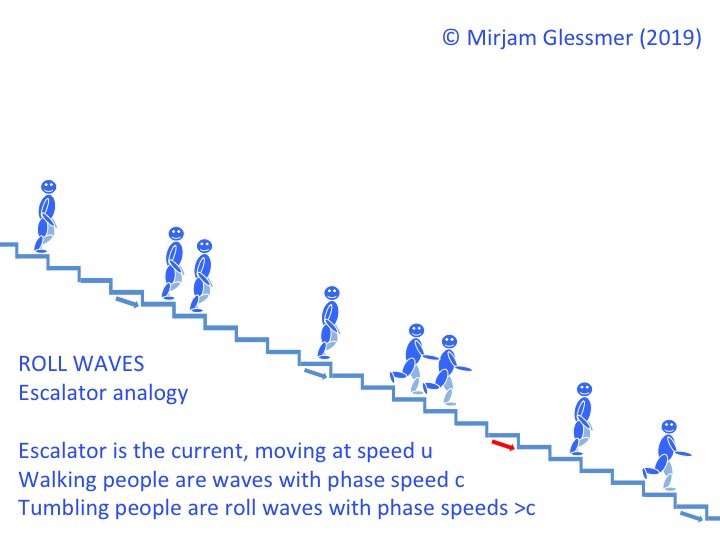
One of the most difficult #friendlywaves I’ve ever gotten! Did I get it right?
Florian sent me a #friendlywave — a wave picture he took, with hopes that I might be able to explain what is going on there. And this one had me puzzled…
Tag: phase speed
Phase and group velocities in deep and shallow water
When Tor came to visit me in GFI’s basement lab a couple of days ago, he told me about an experiment he had seen in Gothenburg in the seventies. So…
Playing with roll wave animations
I love how powerful Powerpoint is, at the same time there surely is a way out there to create these kind of animations with a little less copy & pasting,…
Roll waves, one of the more complicated #friendlywaves I’ve gotten over the years…
#friendlywave is the new hashtag I am currently establishing. Send me your picture of waves, I will do my best to explain what’s going on there! When it rains, it pours,…
Waves on a slope
Earlier this year at Forscherfreizeit Ratzeburg – the summer camp at which Conny, Siska, Martin, a bunch of teenagers and myself spent a week sailing, exploring and playing with water –…
Waves being deflected towards regions of lower phase velocity
Movie of waves being deflected towards regions of lower phase velocity. We are so used to seeing waves behave in a certain way that we usually don’t stop and think…