#friendlywave is the new hashtag I am currently establishing. Send me your picture of waves, I will do my best to explain what’s going on there!

When it rains, it pours, especially in LA. So much so that they have flood control channels running throughout the city even though they are only needed a couple of days every year. But when they are needed, they should be a tourist attraction because of the awesome wave watching to be done there! As you see below, there are waves — with fronts perpendicular to the direction of flow and a jump in surface height — coming down the channel at pretty regular intervals.

Even though this looks very familiar from how rain flows in gutters or even down window panes, having this #friendlywave sent to me was the first time I actually looked into these kinds of flows. Because what’s happening here is nothing like what happens in the open ocean, so many of the theories I am used to don’t actually apply here.

Looks like tidal bores traveling up a river

The waves in the picture above almost look like the tidal bores one might now from rivers like the Severn in the UK (I really want to go there bore watching some day!). Except that bores travel upstream and thus against the current, and in the picture both the flow and the waves are coming at us. But let’s look at tidal bores for a minute first anyway, because they are a good way to get into some of the concepts we’ll need later to understand roll waves, like for example the Froude number.

Froude number: Who’s faster, current or waves?

If you have a wave running up a river (as in: running against the current), there are several different scenarios, and the “Froude number” is often used to characterize them. The Froude number Fr=u/c compares how fast a current is flowing (u) with how fast a wave can propagate (c).

---

Side note: How do we know how fast the waves should be propagating?

The “c” that is usually used in calculating the Froude number is the phase velocity of shallow water waves c=sqrt(gH), which only depends on water depth H (and, as Mike would point out, on the gravitational constant g, which I don’t actually see as variable since I am used to working on Earth). (There is, btw, a fun experiment we did with students to learn about the phase speed of shallow water waves.) This is, however, a problem in our case since we are operating in very shallow water and the equation above assumes a sinusoidal surface, small amplitude and a lot of other stuff that is clearly not given in the see-saw waves we observe. And then this stuff quickly gets very non-linear… So using this Froude number definition is … questionable. Therefore the literature I’ve seen on the topic sometimes uses a different dispersion relation. But I like this one because it’s easy and works kinda well enough for my purposes (which is just to get a general idea of what’s going on).

---

Back to the Froude number.

If Fr<1 it means that the waves propagate faster than the river is flowing, so if you are standing next to the river wave watching, you will see the waves propagating upstream.

Find that hard to imagine? Imagine you are walking on an elevator, the wrong way round. The elevator is moving downward, you are trying to get upstairs anyway. But if you run faster than the elevator, you will eventually get up that way, too! This is what that looks like:

If Fr>1 however, the river is flowing faster than waves can propagate, so even though the waves are technically moving upstream when the water is used as a reference, an observer will see them moving downstream, albeit more slowly than the water itself, or a stick one might have thrown in.

On an escalator, this is what Fr>1 looks like:

But then there is a special case, in which Fr=1.

Hydraulic jumps

Fr=1 means that the current and the waves are moving at exactly the same velocity, so a wave is trapped in place. We see that a lot on weirs, for example, and there are plenty of posts on this blog where I’ve shown different examples of the so-called hydraulic jumps.

See? In all these pictures above there is one spot where the current is exactly as fast as the waves propagating against it, and in that spot the flow regime changes dramatically, and there is literally a jump in surface height, for example from shooting away from where the jet from the hose hits the bottom of the tank to flowing more slowly and in a thicker layer further out. However, all these hydraulic jumps stay in pretty much the same position over pretty long times. This is not what we observe with tidal bores.

On an escalator, you would be walking up and up and up, yet staying in place. Like so:

Roll waves

Tidal bores, and the hydraulic jumps associated with their leading edges, propagate upstream. But they are not waves the way we usually think about waves with particles moving in elliptical orbits. Instead, they are waves that are constantly breaking. And this is how they are able to move upstream: At their base, the wave is moving as fast as the river is flowing, i.e. Fr=1, so the base would stay put. As the base is constantly being pushed back downstream while running upstream at full force, the top of the wave is trying to move forward, too, moving over the base into the space where there is no base underneath it any more, hence collapsing forward. The top of the wave is able to move faster because it’s in “deeper” water and c is a function of depth. This is the breaking, the rolling of those waves. The front rolls up the rivers, entraining a lot of air, causing a lot of turbulent mixing as it is moving forward. And all in all, the whole thing looks fairly similar to what we saw in the picture above from Verdugo Wash.

But the waves are actually traveling DOWN the river

However there is a small issue that’s different. While tidal bores travel UP a river, the roll waves on Verdugo Wash actually travel DOWN. If the current and the waves are traveling in the same direction, what makes the waves break instead of just ride along on the current?

What’s tripping up these roll waves?

Any literature on the topic says that roll waves can occur for Fr>2, so any current that is twice as fast as the speed of waves at that water depth, or faster, will have those periodic surges coming downstream. But why? It doesn’t have the current pulling the base away from underneath it as it has in case of a wave traveling against the current, so what’s going on here? One thing is that roll waves occur on a slope rather than on a more or less level surface. Therefore the Froude number definitions for roll waves include the steepness of the slope — the steeper, the easier it is to trip up the waves.

Shock waves: Faster than the speed of sound

Usually shock waves are defined as disturbances that move faster than the local speed of sound in a medium, which means that it moves faster than information about its impending arrival can travel and thus there isn’t any interaction with a shock wave until it’s there and things change dramatically. This definition also works for waves traveling on the free surface of the water (rather than as a pressure wave inside the water), and describe what we see with those roll waves. Everything looks like business as usual until all of a sudden there is a jump in the surface elevation and a different flow regime surging past.

If you look at such a current (for example in the video below), you can clearly see that there are two different types of waves: The ones that behave the way you would expect (propagating with their normal wave speed [i.e. the “speed of sound”, c] while being washed downstream by the current) and then roll waves [i.e. “shock waves” with a breaking, rolling front] that surge down much faster and swallow up all the small waves in their large jump in surface elevation.

Video by Mike Malaska

In the escalator example, it would look something like this: People walking down with speed c, then someone tumbling down with speed 2c, collecting more and more people as he tumbles past. People upstream of the tumbling move more slowly (better be safe than sorry? No happy blue people were hurt in the production of the video below!).

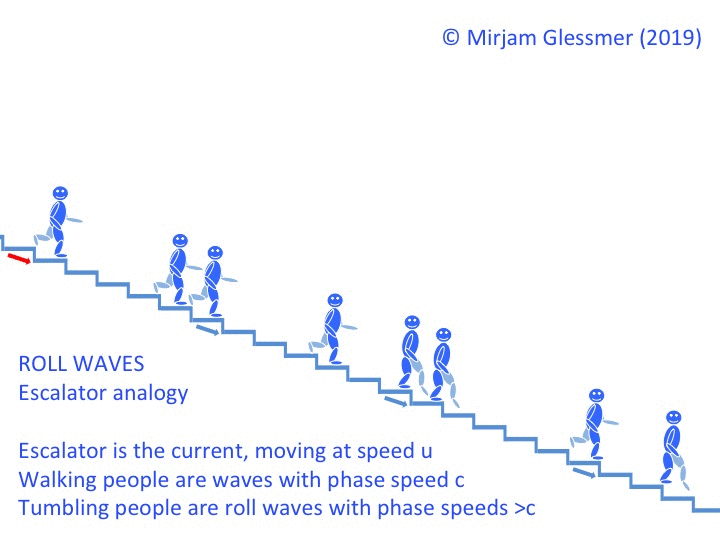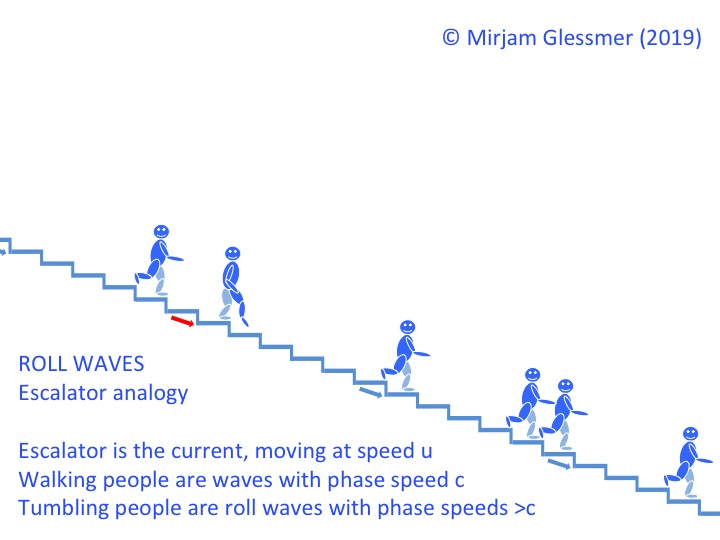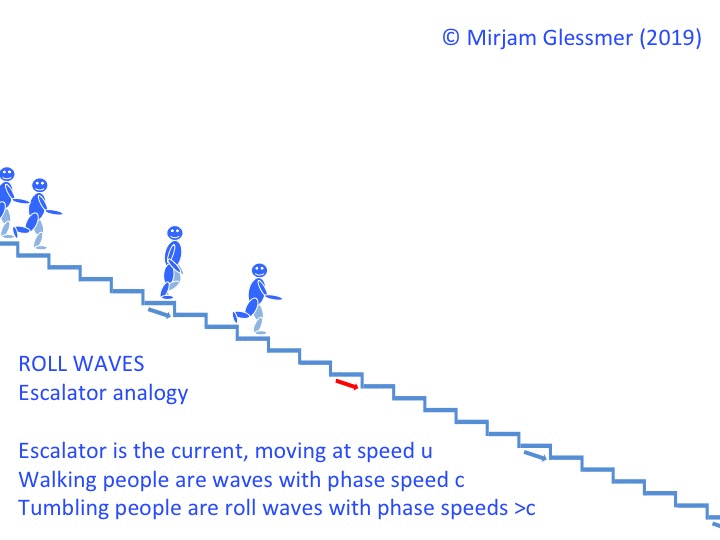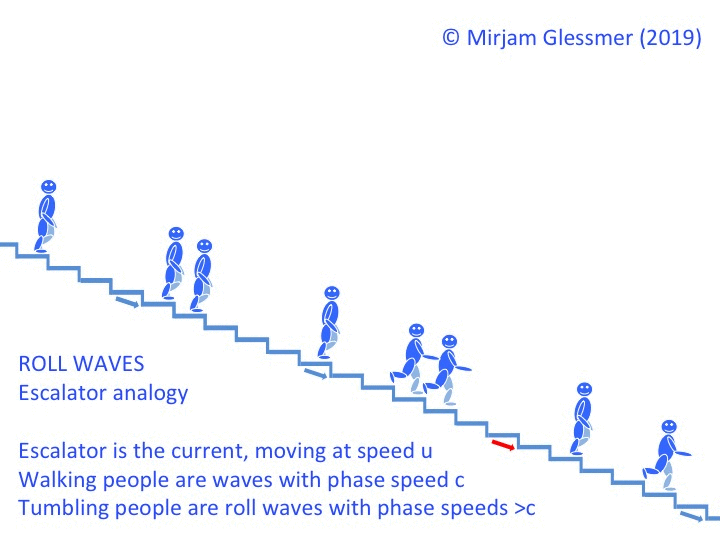
Looking at that escalator clip, it’s also easy to imagine that wave lengths of roll waves become longer and longer the further downstream you go, because as they bump into “ordinary” waves when they are about to swallow them, they push them forward, thus extending their crest just a little more forward. And as the jump in surface height gets more pronounced over time and they collect more and more water in their crests, the bottom drag is losing more and more of its importance. Which means that the roll waves get faster and faster, the further they propagate downstream.

Speaking of bottom drag: When calculating the speed of roll waves, another variable that needs to be considered is the roughness of the ground. It’s easy to see that that would have an influence on shallow water. Explaining that is beyond this blog post, but there are examples in the videos Mike sent me, so I’ll write a blogpost on that soon.

So. This is what’s going on in LA when it is raining. Make sense so far? Great! Then we can move on to more posts on a couple of details that Mike noticed when observing the roll waves, like for example what happens to roll waves when two overflow channels run into each other and combine, or what happens when they hit an obstacle and get reflected.

Thanks for sharing your observations and getting me hooked on exploring this cool phenomenon, Mike!