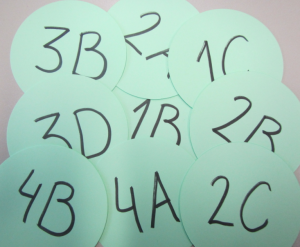Tag Archives: method

Bridging the gap between conventional mathematics teaching and the topics that engineering students are really interested in

1 Reply

I’m very excited to announce that I, together with Christian Seifert, have been awarded a Tandem Fellowship by the Stifterverband für die Deutsche Wissenschaft. Christian, among other things, teaches undergraduate mathematics for engineers, and together we have developed a concept to improve instruction, which we now get support to implement.

The problem that we are addressing is that mathematics is taught to 1300 students from 12 different engineering study programs at once. At the moment, in addition to lectures and practice sessions in both very large and small groups, students get weekly online exercises that they can earn bonus points with. Student feedback is positive – they appreciate the opportunity to practice, they like that they are nudged towards continuously working on whatever is currently going on in class, and obviously they like to earn bonus points they can use on the exam.
However, mathematics is not typically a subject that non-mathematicians are very keen on. Many feel like there is no relevance of the content to their lives or even their studies. And many don’t feel confident they have a chance to succeed.
As I wrote in my recent posts on motivation, both believing that you can succeed and seeing the relevance of things you are supposed to be studying to your life are necessary for people to feel intrinsically motivated. So this is where we want to start.
Since the experience with the weekly online tests is so positive, we want to develop exercises that apply the mathematics they are currently learning to topics from their own, chosen fields. So if they are supposed to practice solving a set of linear equations, students of mechanical engineering, for example, might as well use one from a mechanical engineering case. Or even better: they might be asked to develop this set of equations first, and then solve it. By connecting mathematics with topics students are really interested in, we hope to get them to engage more with matematics.
More engagement will then likely mean that they improve their understanding both of mathmatics itself and – equally important – of their main subjects, where currently manystudents lack the math skills required. At the same time, we hope this will increase student motivation for both subjects.
Of course, there is still a lot of work to be done to first implement this concept and then evaluate whether it is working as well as we thought it would, and then probably modifying it and evaluating some more. But I am excited to get started!

On grading strategies.

Leave a reply

How do you deal with grading to make it less painful?

Talking to a friend who had to grade a lot of exams recently I mentioned a post I had written on how to make grading less painful, only to realize later that I wrote that post, but never actually posted it! So here we go now:

Last semester student numbers in the course I taught went back to less than 1/3rd of the previous year’s numbers. And yet – grading was a huge pain. So I’ve been thinking about strategies that make grading bearable.

The main thing that helps me is to make very explicit rubrics when I design the exam, long before I start grading. I think about what is the minimum requirement for each answer, and what is the level that I would expect for a B. How important are the different answers relative to each other (and hence how many points should they contribute to the final score).

But then when it comes to grading, this is what I do.

I lock myself in to avoid colleagues coming to talk to me and distract me (if at all possible – this year it was not).

I disconnect from the internet to avoid distraction.

I make sure I have enough water to drink very close by.

I go through all the same questions in all the exams before moving on to the next question and looking at that one on all the exams. This helps to make sure grading stays consistent between students.

I also look at a couple of exams before I write down the first grades, it usually takes an adjustment period.

I remind myself of how far the students have come during the course. Sometimes I look back at very early assignments if I need a reminder of where they started from.

I move around. Seriously, grading standing (or at least getting up repeatedly and walking and stretching) really helps.

I look back at early papers I wrote as a student. That really helps putting things into perspective.

I keep mental lists of the most ridiculous answers for my own entertainment (but would obviously not share them, no matter how tempting that might be).

And most importantly: I just do it. Procrastination is really not your friend when it comes to grading…

What do you think? And ideas? Comments? Suggestions? Please share!

Designing exercises with the right amount of guidance as well as the right level of difficulty

Leave a reply

An example of one topic at different levels of difficulty.

Designing exercises at just the right level of difficulty is a pretty difficult task. On the one hand, we would like students to do a lot of thinking themselves, and sometimes even choose the methods they use to solve the questions. On the other hand, we often want them to choose the right methods, and we want to give them enough guidance to be able to actually come to a good answer in the end.

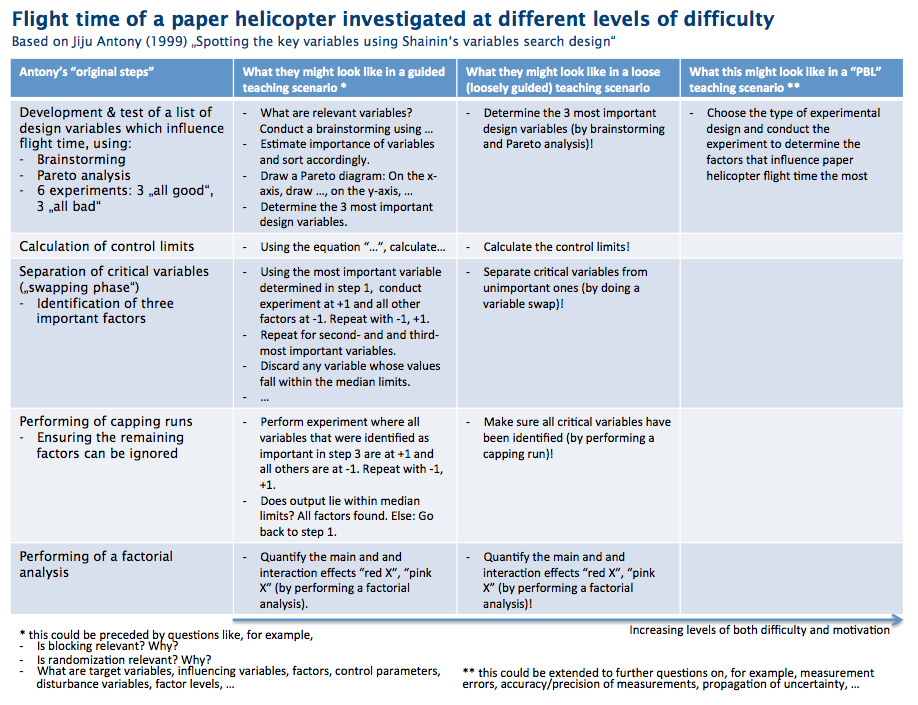
For a project I am currently involved in, I recently drew up a sketch of how a specific task could be solved at different levels of difficulty.

The topic this exercise is on “spotting the key variables using Shainin’s variables search design”, and my sketch is based on Antony’s (1999) paper. In a nutshell, the idea is that paper helicopters (maple-seed style, see image below) have many variables that influence their flight time (for example wing length, body width, number of paper clips on them, …) and a specific method (“Shainin’s variables search design”) is used to determine which variables are the most important ones.

photo-3

Paper helicopter

In the image below, you’ll find the original steps from the Antony (1999) paper in the left column. In the second column, these steps are recreated in a very closely-guided exercise. In the third column, the teaching scenario becomes less strict, (and even less strict if you omit the part in the brackets), and in the right column the whole task is designed as a problem-based scenario.

Screen Shot 2015-01-09 at 15.45.23

Flight time of a helicopter investigated at different levels of difficulty

Clearly, difficulty increases from left to right. Typically, though, motivation of students tasked with similar exercises also increases from left to right.

So which of these scenarios should we choose, and why?

Of course, there is not one clear answer. It depends on the learning outcomes (classified, for example, by Bloom or in the SOLO framework) you have decided on for your course.

If you choose one of the options further to the left, you are providing a good structure for students to work in. It is very clear what steps they are to take in which order, and what answer is expected of them. They will know whether they are fulfilling your expectations at all times.

The further towards the right you choose your approach, the more is expected from the students. Now they will need to decide themselves which methods to use, what steps to take, whether what they have done is enough to answer the question conclusively. Having the freedom to choose things is motivating for students, however only as long as the task is still solvable. You might need to provide more guidance occasionally or point out different ways they could take to come to the next step.

The reason I am writing this post is that I often see a disconnect between the standards instructors claim to have and the kind of exercises they let their students do*. If one of your learning outcomes is that students be able to select appropriate methods to solve a problem, then choosing the leftmost option is not giving your students the chance to develop that skill, because you are making all the choices for them. You could, of course, still include questions at each junction, firstly pointing out that there IS a junction (which might not be obvious to students who might be following the instructions cook-book style), and secondly asking for alternative choices to the one you made when designing the exercise, or for arguments for/against that choice. But what I see  is that instructors have students do exercises similarly to the one in the left column, probably even have them write exams in that style, yet expect them to be able to write master’s theses where they are to choose methods themselves. This post is my attempt to explain why that probably won’t work.

—

* if you recognize the picture above because we recently talked about it during a consultation, and are now wondering whether I’m talking about you – no, I’m not! :-)

Taxonomy of multiple choice questions

Leave a reply

Examples of different kinds of multiple choice questions that you could use.

Multiple choice questions are a tool that is used a lot with clickers or even on exams, but they are especially on my mind these days because I’ve been exposed to them on the student side for the first time in a very long time. I’m taking the “Introduction to evidence-based STEM teaching” course on coursera, and taking the tests there, I noticed how I fall into the typical student behavior: working backwards from the given answers, rather than actually thinking about how I would answer the question first, and then looking at the possible answers. And it is amazing how high you can score just by looking at which answer contains certain key words, or whether the grammatical structure of the answers matches the question… Scary!

So now I’m thinking again about how to ask good multiple choice questions. This post is heavily inspired by a book chapter that I read a while ago in preparation for a teaching innovation: “Teaching with Classroom Response Systems – creating active learning environments” by Derek Bruff (2009). While you should really go and read the book, I will talk you through his “taxonomy of clicker questions” (chapter 3 of said book), using my own random oceanography examples.

I’m focusing here on content questions in contrast to process questions (which would deal with the learning process itself, i.e. who the students are, how they feel about things, how well they think they understand, …).

Content questions can be asked at different levels of difficulty, and also for different purposes.

Recall of facts

In the most basic case, content questions are about recall of facts on a basic level.

Which ocean has the largest surface area?

 

A: the Indian Ocean

B: the Pacific Ocean

C: the Atlantic Ocean

D: the Southern Ocean

E: I don’t know*

Recall questions are more useful for assessing learning than for engaging students in discussions. But they can also be very helpful at the beginning of class periods or new topics to help students activate prior knowledge, which will then help them connect new concepts to already existing concepts, thereby supporting deep learning. They can also help an instructor understand students’ previous knowledge in order to assess what kind of foundation can be built on with future instruction.

Conceptual Understanding Questions

Answering conceptual understanding questions requires higher-level cognitive functions than purely recalling facts. Now, in addition to recalling, students need to understand concepts. Useful “wrong” answers are typically based on student misconceptions. Offering typical student misconceptions as possible answers is a way to elicit a misconception, so it can be confronted and resolved in a next step.

 At a water depth of 2 meters, which of the following statements is correct?

 

A: A wave with a wavelength of 10 m is faster than one with 20 m.

B: A wave with a wavelength of 10 m is slower than one with 20 m.

C: A wave with a wavelength of 10 m is as fast as one with 20 m.

D: I don’t know*

It is important to ask yourself whether a question actually is a conceptual understanding question or whether it could, in fact, be answered correctly purely based on good listening or reading. Is a correct answer really an indication of a good grasp of the underlying concept?

Classification questions

Classification questions assess understanding of concepts by having students decide which answer choices fall into a given category.

Which of the following are examples of freak waves?

 

A: The 2004 Indian Ocean Boxing Day tsunami.

B: A wave with a wave height of more than twice the significant wave height.

C: A wave with a wave height of more than five times the significant wave height.

D: The highest third of waves.

E: I don’t know*

Or asked in a different way, focussing on which characteristics define a category:

Which of the following is a characteristic of a freak wave?

 

A: The wavelength is 100 times greater than the water depth

B: The wave height is more than twice the significant wave height

C: Height is in the top third of wave heights

D: I don’t know*

This type of questions is useful when students will have to use given definitions, because they practice to see whether or not a classification (and hence a method or approach) is applicable to a given situation.

Explanation of concepts

In the “explanation of concepts” type of question, students have to weigh different definitions of a given phenomenon and find the one that describes it best.

Which of the following best describes the significant wave height?

 

A: The significant wave height is the mean wave height of the highest third of waves

B: The significant wave height is the mean over the height of all waves

C: The significant wave height is the mean wave height of the highest tenth of waves

E: I don’t know*

Instead of offering your own answer choices here, you could also ask students to explain a concept in their own words and then, in a next step, have them vote on which of those is the best explanation.

Concept question

These questions test the understanding of a concept without, at the same time, testing computational skills. If the same question was asked giving numbers for the weights and distances, students might calculate the correct answer without actually having understood the concepts behind it.

To feel the same pressure at the bottom, two water-filled vessels must have…

 

A: the same height

B: the same volume

C: the same surface area

D: Both the same volume and height

E: I don’t know*

Or another example:

If you wanted to create salt fingers that formed as quickly as possible and lasted for as long as possible, how would you set up the experiment?

 

A: Using temperature and salt.

B: Using temperature and sugar.

C: Using salt and sugar.

D: I don’t know.*

Ratio reasoning question

Ratio reasoning questions let you test the understanding of a concept without testing maths skills, too.

You are sitting on a seesaw with your niece, who weighs half of your weight. In order to be able to seesaw nicely, you have to sit…

 

A: approximately twice as far from the mounting as she does.

B: approximately at the same distance from the mounting as she does.

C: approximately half as far from the mounting as she does.

D: I don’t know.*

If the concept is understood, students can answer this without having been given numbers to calculate and then decide.

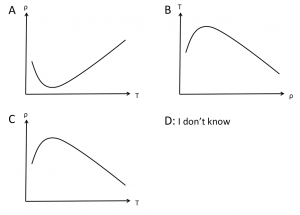
Another type of question that I like:

Which of the following sketches best describes the density maximum in freshwater?

MCQ_questions

If students have a firm grasp of the concept, they will be able to pick which of the graphs represents a given concept. If they are not sure what is shown on which axis, you can be pretty sure they do not understand the concept yet.

Application questions

Application questions further integrative learning, where students bring together ideas from multiple sessions or courses.

Which has the biggest effect on sea surface temperature?

 

A: Heating through radiation from the sun.

B: Evaporative cooling.

C: Mixing with other water masses.

D: Radiation to space during night time.

E: I don’t know.*

Students here have the chance to discuss the effect sizes depending on multiple factors, like for example the geographical setting, the season, or others.

Procedural questions

Here students apply a procedure to come to the correct answer.

The phase velocity of a shallow water wave is 7 m/s. How deep is the water?

 

A: 0.5 m

B: 1 m

C: 5 m

D: 10 m

E: 50 m

F: I don’t know*

Prediction question

Have students predict something to force them to commit to once choice so they are more invested in the outcome of an experiment (or even explanation) later on.

Which will melt faster, an ice cube in fresh water or in salt water?

 

A: The one in fresh water.

B: The one in salt water.

C: No difference.

D: I don’t know.*

Or:

Will the radius of a ball launched on a rotating table increase or decrease as the speed of the rotation is increased?

 

A: Increase.

B: Decrease.

C: Stay the same.

D: Depends on the speed the ball is launched with.

E. I don’t know.*

Critical thinking questions

Critical thinking questions do not necessarily have one right answer. Instead, they provide opportunities for discussion by suggesting several valid answers.

Iron fertilization of the ocean should be…

 

A: legal, because the possible benefits outweigh the possible risks

B: illegal, because we cannot possibly estimate the risks involved in manipulating a system as complex as the ecosystem

C: legal, because we are running a huge experiment by introducing anthropogenic CO2 into the atmosphere, so continuing with the experiment is only consequent

D: illegal, because nobody should have the right to manipulate the climate for the whole planet

For critical thinking questions, the discussion step (which is always recommended!) is even more important, because now it isn’t about finding a correct answer, but about developing valid reasoning and about practicing discussion skills.

Another way to focus on the reasoning is shown in this example:

As waves travel into shallower water, the wave length has to decrease

I. because the wave is slowed down by friction with the bottom.

II. because transformation between kinetic and potential energy is taking place.

III. because the period stays constant.

 

A: only I

B: only II

C: only III

D: I and II

E: II and III

F: I and III

G: I, II, and III

H: I don’t know*

Of course, in the example above you wouldn’t have to offer all possible combinations as options, but you can pick as many as you like!

One best answer question

Choose one best answer out of several possible answers that all have their merits.

Your rosette only lets you sample 8 bottles before you have to bring it up on deck. You are interested in a high resolution profile, but also want to survey a large area. You decide to

 

A: take samples repeatedly at each station to have a high vertical resolution

B: only do one cast per station in order to cover a larger geographical range

C: look at the data at each station to determine what to do on the next station

In this case, there is no one correct answer, since the sampling strategy depends on the question you are investigating. But discussing different situations and which of the strategies above might be useful for what situation is a great exercise.

And for those of you who are interested in even more multiple choice question examples, check out the post on multiple choice questions at different Bloom levels.

—

* while you would probably not want to offer this option in a graded assessment, in a classroom setting that is about formative assessment or feedback, remember to include this option! Giving that option avoids wild guessing and gives you a clearer feedback on whether or not students know (or think they know) the answer.

Asking students to tell us about “the muddiest point”

Leave a reply

Getting feedback on what was least clear in a course session.

A classroom assessment technique that I like a lot is “the muddiest point”. It is very simple: At the end of a course unit, you hand out small pieces of papers and ask students to write down the single most confusing point (or the three least clear points, or whatever you chose). You then collect the notes and go through them in preparation for the next class.

This technique can also be combined with classical minute papers, for example, or with asking students to write down the take-home message they are taking away from that teaching unit. It is nice though if take-home messages actually remain with the students to literally take home, rather than being collected by the instructor.

But give it a try – sometimes it is really surprising to see what students take home from a lesson: It might not be what you thought was the main message! Often they find anecdotes much more telling than all the other important things you thought you had conveyed so beautifully. And then the muddiest points are also really helpful to make sure you focus your energy on topics that students really need help with.

Using the “jigsaw” method for practicing solving problem-sets

1 Reply

A method to get all students engaged in solving problem sets.

A very common problem during problem-set solving sessions is that instead of all students being actively involved in the exercise, in each group there is one student working on the problem set, while the rest of the group is watching, paying more or (more likely) less attention. And here is what you can do to change that:

The jigsaw method (in German often called the “expert” method), you split your class into small groups. For the sake of clarity let’s assume for now that there are 9 students in your class; this would give you three groups with three students each. Each of your groups now get their own problem to work on. After a certain amount of time, the groups are mixed: In each of the new groups, you will have one member of each of the old groups. In these new groups, every student tells the other two about the problem she has been working on in her previous group and hopefully explains it well enough that in the end, everybody knows how to solve all of the problems.

This is a great method for many reasons:

  • students are actively engaged when solving the problem in their first group, because they know they will have to be the expert on it later, explaining it to others who didn’t get the chance to work on this specific problem before
  • in the second set of groups, everybody has to explain something at some point
  • you, the instructor, get to cover more problem sets this way than if you were to do all of them in sequence with the whole group.

How do you make sure that everybody knows which group they belong to at any given time? A very simple way is to just prepare little cards which you hand out to the students, as shown below:

IMG_0314

Cards to help organize the practice and discussion groups

The system then works like this: Everybody first works on the problem with the number they have on their card. Group 1 working on problem 1, group 2 on problem 2, and so forth. In the second step, all the As are grouped together and explain their problems to each other, as are the Bs, the Cs, …

Jigsaw with 9 participants

And what do I do if I have more than 9 students?

This works well with 16 students, too. 25 is already a lot – 5 people in each group is probably the upper limit of what is still productive. But you can easily split larger groups into groups of nine by color-coding your cards. Then all the reds work together, and go through the system described above, as do the blues, the greens, the yellows…

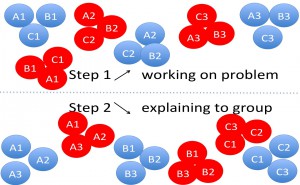
Slide2

Jigsaw with 18 participants in 6 sub-groups of 9 students going through the system as described above

This is a method that needs a little practice. And switching seats to get all students  in the right groups takes time, as does working well together in groups. But it is definitely worth the initial friction once people have gotten used to it!

Creating a continuous stratification in a tank, using the double bucket filling method

2 Replies

Because I am getting sick of stratifications not working out the way I planned them.

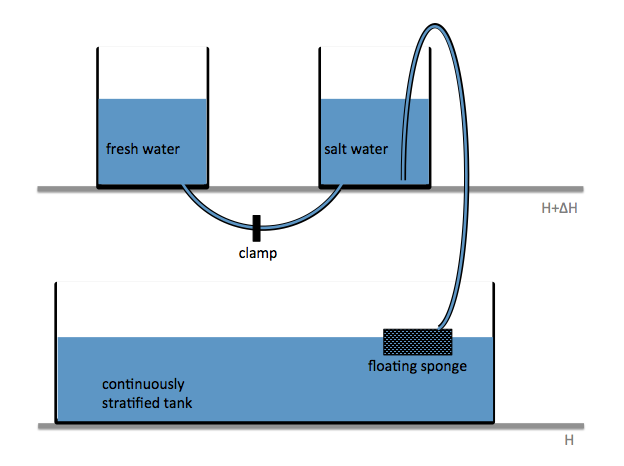
Creating stratifications, especially continuous stratifications, is a pain. Since I wanted a nice stratification for an experiment recently, I finally decided to do a literature search on how the professionals create their stratifications. And the one method that was mentioned over and over again was the double bucket method, which I will present to you today.

Two reservoirs are placed at a higher level than the tank to be filled, and connected with a U-tube which is initially closed with a clamp. Both reservoirs are filled with fresh water. To one of the buckets, salt is added to achieve the highest desired salinity in the stratification we are aiming for. From this bucket, a pump pumps water down into the tank to be filled (or, for the low-tech version: use air pressure and a bubble-free hose to drive water down into the tank as shown in the figure above!); the lower end of the hose rests on a sponge that will float on the water in the tank. When the pump is switched on (or alternatively, the bubble-free hose from the reservoir to the tank opened), the clamp is removed from the U-tube. So for every unit of salt water leaving the salty reservoir through the hose, half a unit of fresh water flows in to keep the water levels in both reservoirs the same height. Thus the salt water is, little by little, mixed with fresh water, so the water flowing out into the tank gets gradually fresher. If all goes well, this results in a continuous salinity stratification.

Things that might go wrong include, but are not limited to,

  • freshwater not mixing well in the saline reservoir, hence the salinity in that reservoir not changing continuously. To avoid that, stir.
  • bubbles in the U-tube (especially if the U-tube is run over the top edges of the reservoirs which is a lot more feasible than drilling holes into the reservoirs) messing up the flow. It is important to make sure there is no air in the tube connecting the two reservoirs!
  • water shooting out of the hose and off the floating sponge to mess up the stratification in the tank. Avoid this by lowering the flow rate if you can adjust your pump, or by floating a larger sponge.

P.S.: For more practical tips for tank experiments, check out the post “water seeks its level” in which I describe how to keep the water level in a tank constant despite having an inflow to the tank.

First day of class – student introductions.

Leave a reply

How do you get students to get to know each other quickly while getting to know them yourself at the same time?

The new school year is almost upon us and we are facing new students soon. For many kinds of classes, there is a huge benefit from students knowing each other well, and from the teacher knowing the students. But how do you achieve that, especially in a large class, without having to spend enormous amounts of class time on it?

There are of course tons of different methods. But one thing that has worked really well for me is to ask a question like “where are you from?” and have people position themselves on an imaginary map (you show which direction is north, but they have to talk to each other to figure out where they have to position themselves relative to the others). For the first question they are usually a bit hesitant, but if you ask three or four, it works really well. For other questions you could ask which of the class topics they are especially interested in, on which topic they have the most knowledge already, or the least, or where they want to go professionally, or what their favorite holiday destination is – all kinds of stuff. Depending on the level of the class, you can ask questions more on the topic of the class or more on a personal level.

This is highly interactive because you always have to talk to people to find your own position, and it is very interesting to see how the most complex configurations of students form, representing maps to scale even though some people might live in the same city whereas other people are from a different continent, for example.

The best thing is that it is a lot easier to remember stuff like “oh, those two used to live really close to where I am from, we were all clustered together for that question”, “those two are interested in exactly the same stuff as I am because they were right next to me when the question was x”, … than to recall that information from when everybody had to introduce themselves one after the other.

I really like this method, give it a try! And don’t be discouraged if students are hesitant at first, they will get into it at the second or third question. And getting them up and moving does wonders for the atmosphere in the room and makes it a lot more comfortable for you, too, to stand in front of a new class.

How to ask multiple-choice questions when specifically wanting to test knowledge, comprehension or application

2 Replies

Multiple choice questions at different levels of Bloom’s taxonomy.

Let’s assume you are convinced that using ABCD-cards or clickers in your teaching is a good idea. But now you want to tailor your questions such as to specifically test for example knowledge, comprehension, application, analysis, synthesis or evaluation; the six educational goals described in Bloom’s taxonomy. How do you do that?

I was recently reading a paper on “the memorial consequences of multiple-choice testing” by Marsh et al. (2007), and while the focus of that paper is clearly elsewhere, they give a very nice example of one question tailored once to test knowledge (Bloom level 1) and once to test application (Bloom level 3).

For testing knowledge, they describe asking “What biological term describes an organism’s slow adjustment to new conditions?”. They give four possible answers: acclimation, gravitation, maturation, and migration. Then for testing application, they would ask “What biological term describes fish slowly adjusting to water temperature in a new tank?” and the possible answers for this question are the same as for the first question.

Even if you are not as struck by the beauty of this example as I was, you surely appreciate that this sent me on a literature search of examples how Bloom’s taxonomy can help design multiple choice questions. And indeed I found a great resource. I haven’t been able to track down the whole paper unfortunately, but the “Appendix C: MCQs and Bloom’s Taxonomy” of “Designing and Managing MCQs” by Carneson, Delpierre and Masters contains a wealth of examples. Rather than just repeating their examples, I am giving you my own examples inspired by theirs*. But theirs are certainly worth reading, too!

Bloom level 1: Knowledge

At this level, all that is asked is that students recall knowledge.

Example 1.1

Which of the following persons first explained the phenomenon of “westward intensification”?

  1. Sverdrup
  2. Munk
  3. Nansen
  4. Stommel
  5. Coriolis

Example 1.2

In oceanography, which one of the following definitions describes the term “thermocline”?

  1. An oceanographic region where a strong temperature change occurs
  2. The depth range were temperature changes rapidly
  3. The depth range where density changes rapidly
  4. A strong temperature gradient
  5. An isoline of constant temperature

Example 1.3

Molecular diffusivities depend on the property or substance being diffused. From low to high molecular diffusivities, which of the sequences below is correct?

  1. Temperature > salt > sugar
  2. Sugar > salt > temperature
  3. temperature > salt == sugar
  4. temperature > sugar > salt

Bloom level 2. Comprehension

At this level, understanding of knowledge is tested.

Example 2.1

Which of the following describes what an ADCP measures?

  1. How quickly a sound signal is reflected by plankton in sea water
  2. How the frequency of a reflected sound signal changes
  3. How fast water is moving relative to the instrument
  4. How the sound speed changes with depth in sea water

Bloom level 3: Application

Knowledge and comprehension of the knowledge are assumed, now it is about testing whether it can also be applied.

Example 3.1

What velocity will a shallow water wave have in 2.5 m deep water?

  1. 1 m/s
  2. 2 m/s
  3. 5 m/s
  4. 10 m/s

Example 3.2

Which instrument would you use to make measurements with if you wanted to calculate the volume transport of a current across a ridge?

  1. CTD
  2. ADCP
  3. ARGO float
  4. Winkler titrator

This were only the first three Bloom-levels, but this post is long enough already, so I’ll stop here for now and get back to you with the others later.

Can you see using the Bloom taxonomy as a tool you would use when preparing multiple-choice questions?

—

If you are reading this post and think that it is helpful for your own teaching, I’d appreciate if you dropped me a quick line; this post specifically was actually more work than play to write. But if you find it helpful I’d be more than happy to continue with this kind of content. Just lemme know! :-)

—

* If these questions were used in class rather than as a way of testing, they should additionally contain the option “I don’t know”. Giving that option avoids wild guessing and gives you a clearer feedback on whether or not students know (or think they know) the answer. Makes the data a whole lot easier to interpret for you!

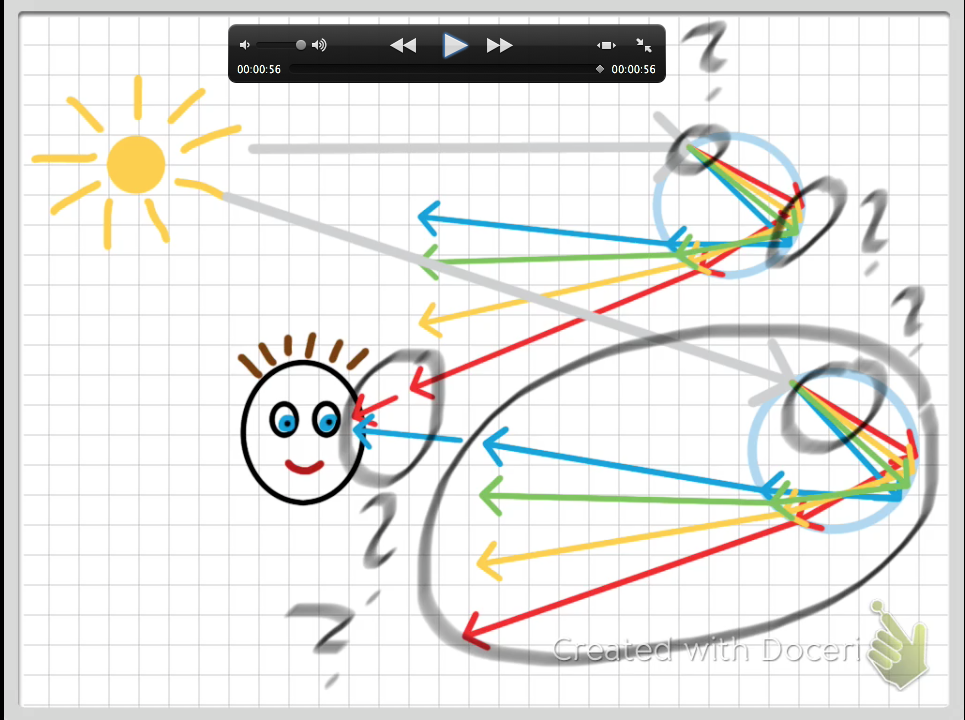
Rainbows and refraction II

1 Reply

Taking the same graphics as in this post, but presenting them differently.

In the previous post, I presented a screen cast explaining, in a very text-booky way, how rainbows form. Today, I am using the same graphics, but I have broken the movie into six individual snippets.

I’m starting out from the schematic that concluded last post’s movie and ask  five questions that you could ask yourself to check whether you understand the schematic:

Ideally I want to link the other five of the movies into the one above, but I haven’t figured out how to do that yet, so here you go for the answers:

What do you think of this way of presenting the material? Do you like it better than the textbook-y movie? I’m curious to hear your opinions!

For both this and the other way of displaying the material, I am toying with the idea of adding quizzes throughout the movies, in a programmed learning kind of way. But considering all the pros and cons, I haven’t made a final decision on it yet. What do you think?