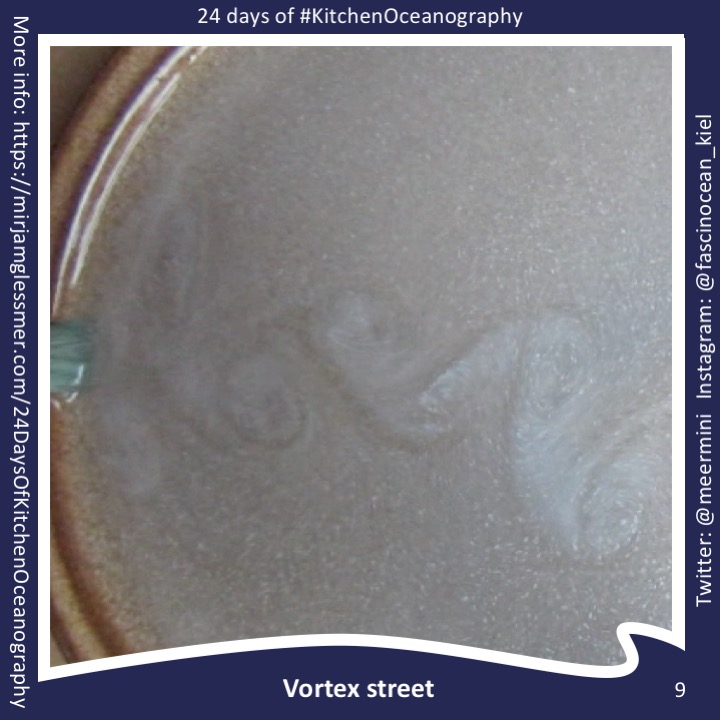
Tag: Karman vortex street

How can we use interactive flow simulations in teaching of hydrodynamics?
That was quite a teaser on Wednesday, wasn’t it? I said I had the solution to any hydrodynamics problem you might want to illustrate. So here we go: I recently had the privilege to be given a private demonstration of the “Elbe” flow solver, which is being developed at Hamburg University of Technology. Elbe allows […]