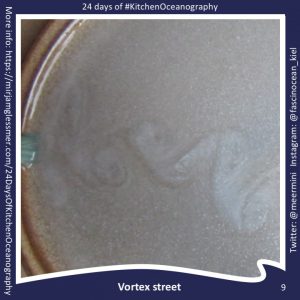
Tag: Karman vortex street


How can we use interactive flow simulations in teaching of hydrodynamics?
That was quite a teaser on Wednesday, wasn’t it? I said I had the solution to any hydrodynamics problem you might want to illustrate. So here we go: I recently…