In earlier posts on drop photography, you might have noticed that the reservoirs for the water that drops out and creates the beautiful liquid art has a weird cork on top, sealing it off, and a glass pipe sticking through. I’ve been wanting to explain what that’s all about for a while, but had to finally draw the picture for our liquid art workshop yesterday. So here we go!
Above, you see Wlodek adjusting something about it, and below is my sketch: A Mariotte’s bottle!
Very useful little thing to control pressure in a reservoir, and with pressure the “reservoir height” that is felt at the outflow, even though the reservoir height is actually changing. Basically, it’s a way to trick the system to feel a constant hydrostatic pressure.
Below on the left, you see the bottle when it has just been filled. A cork is sealing the top of the bottle, except that the inside and outside are connected by a pipe on top and the outflow at the bottom. Initially, the water level inside the top pipe and the bottle are the same and the pressure on both water surfaces is the atmospheric pressure.
As water flows out of the bottle, the water level in the bottle starts sinking. The head space (the air inside the bottle above the water) is sealed off from the outside, so as the water level sinks, its volume increases and its pressure (and thus the pressure on the water surface inside the bottle) sinks. In the middle plot below you see what happens then: The water level inside the pipe starts sinking to compensate for the missing volume inside the bottle.
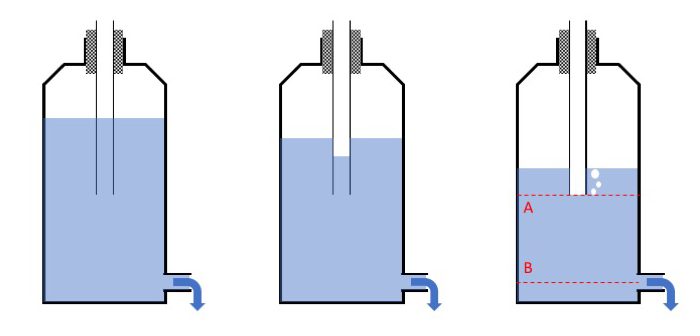
Eventually, air starts bubbling out of the pipe into the headspace, and the water level inside the pipe is at the very bottom end of the pipe (right plot above). The pressure at this level (marked as A) is now atmospheric pressure, not only at the bottom of the pipe, but throughout the whole bottle. And the pressure at this level will continue to stay at atmospheric pressure levels for as long as the water level is still higher than the bottom end of this pipe. Occasionally, air will bubble out of there to compensate for further outflow.
So at the outflow, we always have the hydrostatic pressure relating to the height from B to A, no matter how much or little water there is in the reservoir. That means that all drop pictures in a series will have similar conditions, even as the reservoir is slowly getting empty. How cool is that? I love those kind of things. So simple, yet so efficient! :-)



