Tag Archives: mathematics

How to know for sure whether a teaching intervention actually improved things

Leave a reply

How do we measure whether teaching interventions really do what they are supposed to be doing? (Spoiler alert: In this post, I won’t actually give a definite answer to that question, I am only talking about a paper I read that I found very helpful, and reflecting on a couple of ideas I am currently pondering. So continue reading, but don’t expect me to answer this question for you! :-))

As I’ve talked about before, we are currently working on a project where undergraduate mathematics and mechanics teaching are linked via online practice problems. Now that we are implementing this project, it would be very nice to have some sort of “proof” of its effectiveness.

My (personal) problem with control group studies
Control group studies are likely the most common way to “scientifically” determine whether a teaching intervention had the desired effect. This has rubbed me the wrong way for some time — if I am so convinced that I am improving things, how can I keep my new and improved course from half of the students that I am working to serve? Could I really live with myself if we, for example, measured that half of the students in the control group dropped out within the first three or four weeks of our undergraduate mathematics course, while of the experimental group, only much fewer students dropped out, and much later in the semester? On the other hand, if our intervention had such a large effect, shouldn’t we be measuring it (at least once) in a classical control group study, so we know for sure what its effect is, in order to convince stakeholders at our and other universities that our intervention should be adopted everywhere? If the intervention really improves this much, everybody should see the most compelling evidence so that everybody starts adopting the intervention, right?

A helpful article
Looking for answers to the questions above, I asked Nicki for help, and she pointed me to a presentation by Nick Tilley (2000), that I found really eye-opening and helpful for framing those questions differently, and starting to find answers. The presentation is about evaluation in a social sciences context, but easily transferable to education research.

In this presentation, Tilley first places the proposed method of “realistic evaluation” in the larger context of philosophy of science. For example Popper (1945) suggests using small-scale interventions to deal with specific problems instead of large interventions that address everything at once, and points to the opportunities to investigate the extent to which the theories (on which those small-scale interventions were built) can be tested and improved. Similarly, Campbell (1999) talks about “reforms as experiments”. So the “realistic evaluation” paradigm has been around for a while, partly in conflict with how we do science “conventionally”.

Reality is too complex for control group studies
Then, Tilley talks about classical methods, specifically control group experiments, and argues that — in contrast to what is portrayed in washing detergent ads, for example — studys are typically too complex to directly transfer results between different contexts. In contrast to what science typically does, we are also not investigating a law of nature, where the goal is to understand a mechanism causing a regularity in a given context. Rather, we are investigating how we can cause a change in a regularity. This means we are asking the question “what works for whom in what circumstances?”. With our intervention, we might be introducing different mechanisms, triggering a change in balance of several mechanisms, and hence change the regularities under investigation (which, btw, is our goal!) — all by changing the context.

The approach for evaluations of interventions should therefore, according to Tilley, be “Context Mechanism Outcome Configurations” (CMOC), which describe the interactions between context, mechanism and outcome. In order to create such a description, one needs to clearly describe the mechanisms (“what is it about a measure which may lead it to have a particular outcome pattern in a given context?”), context (“what conditions are needed for a measure to trigger mechanisms to produce particular outcome patterns?”), outcome pattern (“what are the practical effects produced by causal mechanisms being triggered in a given context?” and this finally leads to CMOCs (“How are changes in regularity (outcomes) produced by measures introduced to modify the context and balance of mechanisms triggered?”).

Impact of CCTV on car crimes — a perfect example for control group studies?
Tilley gives a great example for how this works. Investigating how CCTV affects rates of car crimes seems to be easily measured by a classical control group setup. Just install the cameras and compare their crime rates with those of parking spaces without cameras! However, once you start thinking about mechanisms through which the CCTV cameras could influence crime rates, there are lots of different possible mechanisms. There are eight named explicitly in the presentation, for example offenders could be caught thanks to CCTV and go to jail, hence crime rates would sink. Or, criminals might not choose to commit crimes, because the risk of being caught increased due to CCTV, which would again result in lower crime rates. Or people using the car park might feel more secure in using it and therefore start using it more, making it busier at previously less busy times, making car theft more difficult and risky, leading to sinking crime rates.

But then, we also need to think about context, and how car parks and car park crimes potentially differ. For example, crime rate can be the same whether there are a few very active criminals, or many not as busy ones. So catching the similar number of offenders might have a different effect, depending on context. Or the pattern of usage of car parks might depend on working hours of people working close by. So if the dominant CCTV mechanism would be to increase confidence in usage, this would not really help because the busy hours are dedicated by people’s schedules, not how safe they feel. If this would lead to higher usage, however, more cars being around might mean more car crimes because there are more opportunities, yet still a decreased crime rate per use. Another context would be that thieves might just look for new targets outside of the one car park that is now equipped with CCTV, thereby just displacing the problem elsewhere. And there are a couple more contexts mentioned in the presentation.

Long story short: Even for a relatively simple problem (“how does CCTV affect car crime rate?”), there is a wide range of mechanisms and contexts which will all have some sort of influence. Just investigating one car park with CCTV and a second one without will likely not lead to results that help solve the car crime issue once and for all everywhere. First, theories of what exactly the mechanisms and contexts are for a given situation need to be developed, and then other methods of investigation are needed to figure out what exactly is important in any given situation. Do people leave their purses sitting out visibly in the same way everywhere? How are CCTV cameras positioned relative to the cars being stolen? Are usage pattern the same in two car parks? All of this and more needs to be addressed to sort out which of the context-mechanism theories above might be dominant at any given car park.

Back to mathematics learning and our teaching intervention
Let’s get back to my initial question that, btw, is a lot more complex than the example given in the Tilley-presentation. How can we know whether our teaching intervention is actually improving anything?

Mechanisms at play
First, let’s think about possible mechanisms at play here. “What is it about a measure which may lead it to have a particular outcome pattern in a given context?” Without claiming that this is a comprehensive list, here are a couple of ideas:
a) students might realize that they need mathematics to work on mechanics problems, increasing their motivation to learn mathematics
b) students might have more opportunity to receive feedback than before (because now the feedback is automated), and more feedback might lead to better learning
c) students might appreciate the effort made by the instructors, feel more valued and taken seriously, and therefore be more motivated to put in effort
d) students might prefer the online setting over classical settings and therefore practice more
e) students might have more opportunity to practice because of the flexibility in space and time given by the online setting, leading to more learning
f) students might want to earn the bonus points they receive for working on the practice problems
g) students might find it easier to learn mathematics and mechanics because they are presented in a clearer structure than before

Contexts
Now contexts. “What conditions are needed for a measure to trigger mechanisms to produce particular outcome patterns?” Are all students and all student difficulties with mathematics the same? (Again, this is just a spontaneous brain storm, this list is nowhere near comprehensive!)
– if students’ motivation to learn mathematics increased because they see that they will need it for other subjects (a), this might lead to them only learning those topics where we manage to convey that they really really need them, and neglecting all the topics that might be equally important but where we, for whatever reasons, just didn’t give as convincing an example
– if students really value feedback this highly (b), this might work really well, or there might be better ways to give personalised feedback
– if students react to feeling more valued by the instructor (c), this might only work for the students who directly experienced a before/after when the intervention was first introduced. As soon as the intervention has become old news, future cohorts won’t show the same reaction any more. It might also only work in a context where students typically don’t feel as valued so that this intervention sticks out
– if students prefer the online setting over classical settings generally (d), or appreciate the flexibility (e), this might work for us while we are one of the few courses offering such an online setting. But once other courses start using similar settings, we might be competing with others, and students might spend less time with us and our practice problems again
– if students mainly work for the bonus points (f), their learning might not be as sustainable as if they were intrinsically motivated. And as soon as there are no more bonus points to be gained, they might stop using any opportunity for practice just for practice’s sake
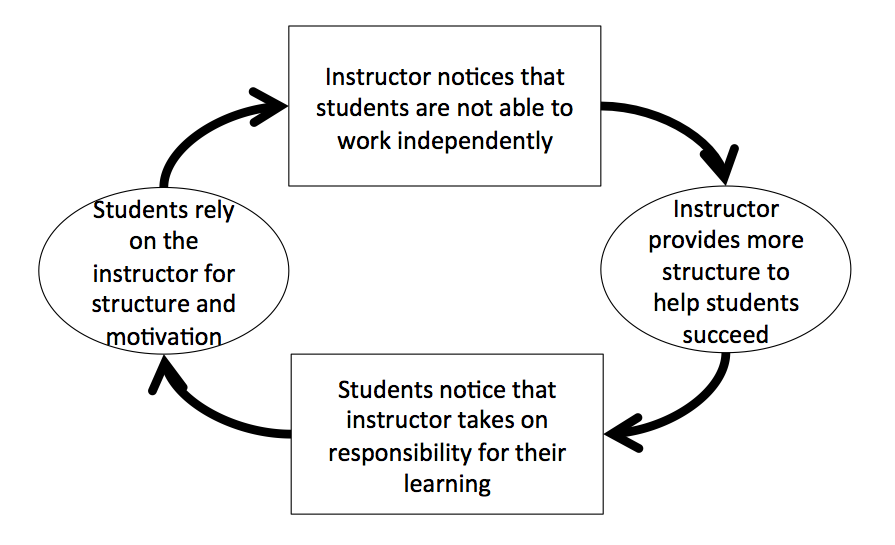
– providing students a structure (g) might make them depend on it, harming their future learning (see my post on this Teufelskreis).

Outcome pattern
Next, we look at outcome patterns: “what are the practical effects produced by causal mechanisms being triggered in a given context?”. So which of the mechanisms identified above (and possibly others) seem to be at play in our case, and how do they balance each other? For this, we clearly need a different method than “just” measuring the learning gain in an experimental group and compare it to a control group. We need a way to identify the mechanisms at play in our case, and those that are not. We then need to figure out the balance of those mechanisms. Is the increased interest in mathematics more important than students potentially being put off by the online setting? Or is the online setting so appealing that it compensates for the lack of interest in mathematics? Can we show students that we care about them without rolling out new interventions every semester, and will that motivate them to work with us? Do we really need to show the practical application of every tiny piece of mathematics in order for students to want to learn it, or can we make them trust us that we are only teaching what they will need, even if they aren’t yet able to see what they will need it for?

This is where I am currently at. Any ideas of how to proceed?

CMOCs
And finally, we have reached the CMOCs (“How are changes in regularity (outcomes) produced by measures introduced to modify the context and balance of mechanisms triggered?”). Assuming we have identified the outcome patterns, we would need to figure out how to change those outcome patterns, either by changing the context, or by changing the balance of mechanisms being triggered.

After reading this article and applying the concept to my project (and I only read the article today, so my thoughts will hopefully evolve some over the next couple of weeks!), I feel that the control group study that everybody seems to expect from us is not as valid as most people might think. As I said above, I don’t have a good answer yet for what we should do instead. But I found it very eye-opening to think about evaluations in this way and am confident that we will figure it out eventually! Luckily we have only run a small-scale pilot at this point, and there is still some time before we start rolling out the full intervention.

What do you think? How should we proceed?

Can you make “boring” math or physics exciting by relating it to the adventures of a research cruise in Antarctic? Elin can!

Leave a reply

My friend Elin is currently on a research cruise in Antarctica and you really need to check out her blog. She is writing about life at sea, including the most beautiful photos of sea ice. Today’s post is called “ice or no ice” and describes the first couple of days of the research cruise. Elin combines the catching narrative with exercises and experiments that will be conducted by at least 30 schools all over Norway! And maybe you can use some of her posts, exercises and experiments in your teaching, too?

Today, for example, the exercises are all about ice. Depending on how much brain power you want to invest and how much prior knowledge your students have, you could for example do an exercise about Archimedes’ principle, calculating how much of an ice floe is visible above the water’s surface, and how many scientists you could put on it before people start getting wet feet. Or, more challenging, you could work with real data that Elin provides to practice your statistics and look at the annual cycle of sea ice in Antarctica. Or you could even set up differential equations for how ice thickness increases over time.

There will be new exercises every Monday for the next two months. How exciting!

Elin’s blog, “På tokt i Antarktis“, is available in English, Norwegian and Swedish. So you can use it not only to practice your maths and physics, but also your language skills! :-)

Btw, if you got hooked and can’t nearly get enough of reading about that research cruise, there is a second blog that tells you, for example, about the different kind of New Year’s Eve the scientists and crew had before heading off to Antarctica. Also very much worth a read!

LA03_Pfannkucheneis_klein

Why you should shuffle practice problems rather than blocking them

3 Replies

We like to get into the flow when practicing something, and we like to have our students concentrate on one particular type of problem at a time until they have mastered it, before moving on to the next. But is that really the best way of learning? Spoiler alert: It is not!

In a 2014 study, Rohrer, Dedrick and Burgess show the benefits of interleaved mathematics practice for problems that are not superficially similar. If problems are superficially similar, it makes intuitive sense that one needs to – at least at some point – practice several types together, because clearly distinguishing different kinds of problems and choosing the appropriate approach to solving it is not easy since the problems themselves look so similar. But for problems that look already very different one might think that blocking similar problems and practicing on them until they are mastered, and then moving on to the next type of problem might be a good choice, since one can really concentrate on each type individually and make sure one masters it.

However, this is not what the data shows. Mean test scores in their study (on an unannounced test two weeks after a nine-week practice period) were twice as high for students who had practiced interleaved problems than for those who had been objected to blocked study. Why is that the case?

There are many possible reasons.

One not even connected to interleaving or blocking is that the spacing effect comes into play: just by learning about a topic spaced in chunks over a longer period of time, the learning gain will be higher.

But interleaving itself will help students learn to distinguish between different kinds of problems. If all problems students encounter in any given lesson or homework assignment are of the same kind, they cannot learn to distinguish this kind of problem from other kinds. Being able to distinguish different kinds of problems, however, is obviously necessary to pick the appropriate strategy to solving a problem, which in itself is obviously necessary to actually solving the problem.

So why can’t student learn this in blocked practice? For one, they don’t even need to look for distinguishing features of a given problem if they know that they will find its solution by applying the exact same strategy they used on the problems before, which will also work for the problems after. So they might get a lot of practice executing a strategy, but likely will not learn under which circumstances using this strategy is appropriate. And the strategy might even just be held in short-term memory for the duration of practice and never make it into long term memory since it isn’t used again and again. So shuffling of types of problems is really important to let students both distinguish different types of problems, and associate the correct strategy to solving each type.

If you are still not convinced, there is another study by Rohrer and Taylor (2007) that shows part of what you might be expecting: That practice performance of “blockers” (i.e. students who practice in blocks rather than mixed) is substantially higher than that of “mixers”. Yet, in a later test on all topics, mixers very clearly outperformed blockers here, too.

So what does that mean for our teaching? Shuffle practice problems and help students learn how to discriminate between different kinds of problems and associate the right approach to solving each kind!

—

Rohrer, D., & Taylor, K. (2007). The shuffling of mathematics problems improves learning Instructional Science, 35 (6), 481-498 DOI: 10.1007/s11251-007-9015-8

Rohrer D., Dedrick R.F., & Burgess K. (2014). The benefit of interleaved mathematics practice is not limited to superficially similar kinds of problems. Psychonomic bulletin & review, 21 (5), 1323-30 PMID: 24578089

Will giving your students more structure make them need more structure?

Leave a reply

One of the arguments against offering students practice opportunities online and providing automated feedback right then and there is that that way, they will never learn to work independently. Since I am working on e-assessment a lot and with many different courses at the moment, this is a fear that I definitely need to take seriously. I don’t believe that the danger is as big as it is sometimes made out to be, but I do believe that there is a vicious circle to be aware of.

It all starts with the instructor having the impression that students are not able to organize their learning on their own. Since the instructor wants the students to succeed, she offers them a clear structure, possibly with bonus points or other kinds of rewards, so they have a safe space with instantaneous feedback to practice skills that are required later. So far, so good.
Now the students are given this structure, and get used to working on problems that are presented in small portions and with instantaneous feedback. They start believing that it is the instructor’s job to organize their learning in such a way, and start relying on the instructor to provide both motivation and bite-sized exercises.
Which the instructor, in turn, notices and interprets as the students becoming less and less able to structure their learning.
At this point it is very easy to fall in the trap of trying to provide an even better, more detailed, structure, so that the students have a better chance of succeeding. Which would likely lead to the students relying even more heavily on the instructor for structure and motivation.
Teufelskreis

It is easy to fall into a vicious circle where the instructor feels like they need to provide more and more structure and motivation, and the students feel less and less responsible for their own learning.

So what can we do? On the one hand we want to help students learn our content, on the other hand they also need to learn to learn by themselves. Can both happen at the same time?
I would say yes, they can.
The first step is recognizing the danger of entering into this downward spiral. There is absolutely no point in hoping that the students will take the initiative and not fall into the trap of relying on us, even if we point out that the trap is there. Of course they might not fall in, but whether they do or not is beyond our influence. We can only directly influence our own actions, not the students’, so we need to make sure to break the spiral ourselves.
The second step is to make sure that we resist the urge to give more and more detailed exercises and feedback.
The third step is to create an exit plan. Are we planning weekly quizzes as homework that students get a certain number of bonus points for? Then we should make sure that over time, either the number of bonus points will decrease, the time interval will become longer, the tasks become more difficult, or a combination of all three. The idea is to reward the behaviour we want just long enough that students establish it, but not any longer than that.
And of course, last but not least, instead of giving students more structure, we can help them learn the tools they need to organize their learning. Be it training skills to organize yourself, or helping them find intrinsic motivation, or teaching them to ask the right questions so they can walk themselves through complex problems until they find an answer.
It’s a pretty thin line to walk, and especially the fourth step might really be out of an instructor’s control when there is a lot of content to go through in very little time and the instructor isn’t the one deciding how much time is going to be spent on which topic. Most TAs and even many teaching staff won’t have the freedom to include teaching units on learning learning or similar. Nevertheless, it is very important to be aware of the vicious circle, or of the potential of accidentally entering it, to be sure that our best intentions don’t end up making students depending on us and the structures we provide, but instead make them independent learners.

Bridging the gap between conventional mathematics teaching and the topics that engineering students are really interested in

1 Reply

I’m very excited to announce that I, together with Christian Seifert, have been awarded a Tandem Fellowship by the Stifterverband für die Deutsche Wissenschaft. Christian, among other things, teaches undergraduate mathematics for engineers, and together we have developed a concept to improve instruction, which we now get support to implement.

The problem that we are addressing is that mathematics is taught to 1300 students from 12 different engineering study programs at once. At the moment, in addition to lectures and practice sessions in both very large and small groups, students get weekly online exercises that they can earn bonus points with. Student feedback is positive – they appreciate the opportunity to practice, they like that they are nudged towards continuously working on whatever is currently going on in class, and obviously they like to earn bonus points they can use on the exam.
However, mathematics is not typically a subject that non-mathematicians are very keen on. Many feel like there is no relevance of the content to their lives or even their studies. And many don’t feel confident they have a chance to succeed.
As I wrote in my recent posts on motivation, both believing that you can succeed and seeing the relevance of things you are supposed to be studying to your life are necessary for people to feel intrinsically motivated. So this is where we want to start.
Since the experience with the weekly online tests is so positive, we want to develop exercises that apply the mathematics they are currently learning to topics from their own, chosen fields. So if they are supposed to practice solving a set of linear equations, students of mechanical engineering, for example, might as well use one from a mechanical engineering case. Or even better: they might be asked to develop this set of equations first, and then solve it. By connecting mathematics with topics students are really interested in, we hope to get them to engage more with matematics.
More engagement will then likely mean that they improve their understanding both of mathmatics itself and – equally important – of their main subjects, where currently manystudents lack the math skills required. At the same time, we hope this will increase student motivation for both subjects.
Of course, there is still a lot of work to be done to first implement this concept and then evaluate whether it is working as well as we thought it would, and then probably modifying it and evaluating some more. But I am excited to get started!