On vorticity
I’ve promised a long time ago to write a post on vorticity (Hallo Geli! :-)). So here it comes!
Vorticity is one of the concepts in oceanography that is often taught via its mathematical formulation, and which is therefore pretty difficult to grasp for those of us with less mathematical training. But it’s also a concept that you can have an intuitive grasp of, and I’ll try to show you how.
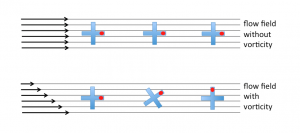
The easiest way to imagine what “vorticity” is, is to think of a little float in a flow. In a vorticity-free flow, that little float will always keep its orientation (see below). However if there is a shear in the flow, i.e. the flow field carries vorticity, it will start to turn.
Flow fields without vorticity (top) and with vorticity (bottom).
This even holds true for vortices: There are vorticity-free vortices as well as those that carry vorticity (as the name “vortex” would suggest).
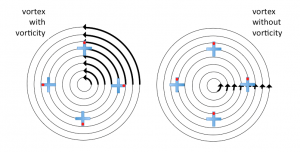
Vorticity-laden and vorticity-free vortex. In the left plot, angular velocity of all particles is the same. In the right plot, angular velocity increases the closer you get to the center of the vortex.
If you think back to the discussion on a tank spinning up to reach solid body rotation, you might recognize that only the vortex with vorticity moves like a solid body. To me, a solid body is basically a fluid with so much friction in it, that molecules cannot change their position relative to each other. And that serves as my memory hook for one condition for the formation of vorticity – the flows must have viscous forces and friction in it.
This sounds very theoretical, but there are a lot of instances where you can spot vorticity in real life, for example twigs caught up twirling in eddies at the edge of streams are clearly moving in a vorticity-filled environment. Below, for example, the stream is clearly not vorticity-free.
Did this help a little? Or what else might help?
Tilting the ice shelf! Or: Our experiments are getting more realistic – Elin Darelius & team's scientific adventures says:
[…] a quick explanation of vorticity see this blog post — quick and dirty explanation is that if water depth changes, a water column will change its […]
What happens when a current meets an obstacle? Topographic steering – Elin Darelius & team's scientific adventures says:
[…] of constant potential vorticity (ω+f)/H. In this, ω is the rotation of the fluid (more on this here), f is the Coriolis parameter, and H is the water depth. So if a current is flowing straight […]
Tilting the ice shelf! Or: Our experiments are getting more realistic – Mirjam S. Glessmer says:
[…] a quick explanation of vorticity see this blog post — quick and dirty explanation is that if water depth changes, a water column will change its […]
What happens when a current meets an obstacle? Topographic steering – Mirjam S. Glessmer says:
[…] of constant potential vorticity (ω+f)/H. In this, ω is the rotation of the fluid (more on this here), f is the Coriolis parameter, and H is the water depth. So if a current is flowing straight […]
What happens when a current meets an obstacle? Topographic steering – Elin Darelius & Team says:
[…] of constant potential vorticity (ω+f)/H. In this, ω is the rotation of the fluid (more on this here), f is the Coriolis parameter, and H is the water depth. So if a current is flowing straight […]