
So what exactly are we testing?
Asking the right questions is really difficult.
Last week, a paper by Gläser and Riegler was presented in the journal club at my work (can’t find it online yet, so can’t link to it, sorry!). Even though the paper itself dealt with the effectiveness of so-called “Brückenkurse” (i.e. 2-week courses that are offered to incoming students to bring them up to speed in mathematics before they take up their regular university courses), what ended up fascinating me much more is how one the choice of the test question was really unfortunate.
The authors were trying to compare additive and proportional reasoning capabilities of the students. Additive reasoning is of the kind “if M and G share a cake and M eats 2/3rd of it, how much does G get?” or “If you want to be at school five minutes earlier than usual, how much earlier than usual should you be leaving from home?”. Proportional reasoning, on the other hand, is something like “M is driving at constant speed. After one hour, she has driven 15km. How far had she driven after 30 minutes?”. Browsing now, I see that there is tons of literature on how children develop additive and proportional reasoning skills which I haven’t read yet, so please go look for yourself if you want to know more about that.
Anyway, the question the authors asked to gauge the additive reasoning skills of the students, went something like this:
A rectangle with a diagonal length of 2 cm is uniformly scaled up, such that its circumference grows by 2.5 cm. The new diagonal is now 3 cm long. Now a similar rectangle, with a 7cm long diagonal, is scaled up such that its circumference grows by 2.5 cm. How long is the diagonal of the new rectangle?
And then they offer multiple choice answers for both the result and the explanations.
Wanna figure it out for yourself? Go ahead! I won’t talk about the answer until much further down in the figure caption…
We did not actually solve this question during the discussion, but the ideas bounced around all focussed on “a2 + b2 = c2” or “sine and cosine!” or other stuff prompted by a right triangle – likely the kind of associations that students taking that test would also have.
Since we weren’t aware that we were looking at a question to be solved with additive reasoning, the simplest solution didn’t occur to us. Maybe not surprisingly, since similarity in geometry means that one shape can be produced from another only by stretching and/or rotating and/or flipping it, with all angles staying the same and the proportion of all lengths staying the same, too, which seems to be all about proportionality rather than additive reasoning.
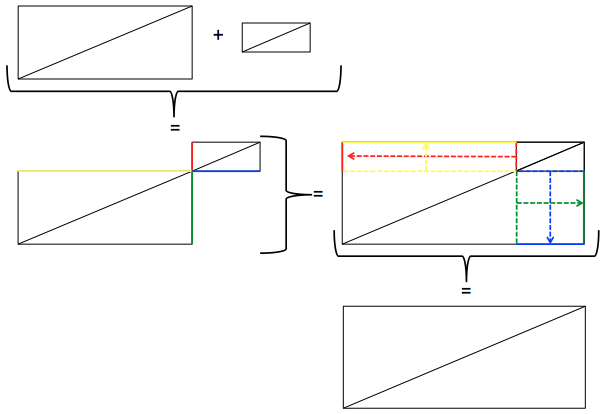
The main steps in discovering that additive reasoning actually works in this case. From the question we know that adding a similar rectangle with 2.5 cm circumference increased the diagonal by 1 cm, from the drawing above we see that this holds no matter the size of the original rectangle as long as similarity is given (which it is in the question), hence the length of the diagonal in the question will increase from 7 to 8 cm.
Looking for an additive reasoning solution, in the end that one is very easy to find (see figure above). However, looking at those exercises was a great reminder for how much we are conditioned to react to certain stimuli in specific ways. See a right triangle? a2 + b2 = c2! Mathematics test? Must be some complicated solution and not just straight-forward adding up of two numbers! There is a lot of research on how correct problem-solving strategies are triggered in situations where they are not applicable, but it was a good (and scary!!) reminder to experience first hand how none* of us 15 or so colleagues came up with the correct strategy right away to solve this really very simple problem. This really needs to have implications on how we think about teaching, especially on how we condition students to react to clues as to what kind of strategy they should pick to solve a given problem. Clearly it is important to have several strategies ready at hand and to think a little bit about which one is applicable in a given situation, and why.
—
* edit: apparently one colleague did come up with the correct answer for the correct reasons, but didn’t let the rest of us know! Still – one out of 14 is a pretty sobering result.