Tag Archives: literature

Motivation proportional to the expectation of achieving a goal?

2 Replies

In the last post I talked about a paper on “Motivating Learners: A Primer for Engineering Teaching Assistants” by Torres-Ayala and Herman (2012). Today, I want to present a different motivation theory, also described in that paper:

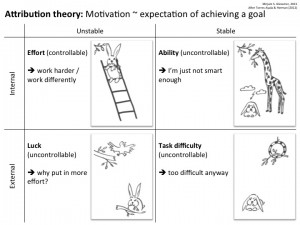
Attribution theory

Attribution theory basically says that motivation is proportional to the expectation of achieving a goal. Three different factors come into play: externality, stability and controllability. So there are basically four different mindsets students can have:

The most desirable one is one that places an emphasis on effort. Students believe that their chance for success is something internal and unstable, which means that since it is determined within themselves and is not fixed, it can be changed. So they know that if they work harder (or work differently), they can be successful. Since their fate is in their own hands, it is easy to be motivated to do your best.

Other students focus on their ability. This is not desirable, because while they still perceive their chance for success as something that is determined within themselves, they also think that they cannot influence whether they are successful or not. They typically feel like they are not smart enough (or — almost as bad — that they are so smart that everything has to go their way, no matter how much effort they put into it).

A third group of students focusses on task difficulty. Task difficulty is obviously determined externally and is stable – students are likely to feel like the exam was too difficult anyway and they had no chance of controlling whether or not they would be successful.

And then lastly, students that feel that their success depends on luck. Luck is also external, and it is unstable. They don’t know whether they will be lucky or not, but in any case they feel like there is no point putting in an effort.

Folie2

My illustration of attribution theory of motivation

How does knowing about attribution theory help us improve our teaching?

When we know that students are basically only motivated when they feel like they have a direct influence on whether or not they will be successful, we should try and create an environment where learners do feel like that. That means fostering a growth mindset, i.e. not focussing on student abilities, but making sure they realize that they can learn whatever they chose if they put in the effort. It also means making sure that students can rely on the environment being exactly like you said it would be, meaning that if you say you won’t call on people which didn’t raise their hands, you can absolutely not do it. And it also means that students cannot get the impression that you favor some over the others, or that your mood and your grades depend on the weather. Lastly, it means that the task difficulty has to be appropriate. Some challenge is good, but if students don’t have a chance to succeed, they will not continue trying indefinitely (in fact, most quit a lot faster than expected). And who can blame them when their chances of success aren’t more or less proportional to the amount of effort they put in?

—
Ana T. Torres-Ayala, & Geoffrey L. Herman (2012). Motivating Learners: A Primer for Engineering Teaching Assistants American Society for Engineering Education

Motivation: dangle a carrot rather than threaten with a whip!

2 Replies

Why do students engage in academic tasks?

Next week I am giving a workshop on teaching large classes at TU Dresden. I gave a similar workshop there in spring, but because of its success I’ve been given twice as much time this time around. So there is a lot of exciting content that I can add to the (obviously already exciting!) workshop ;-)

When preparing what I want to talk about, I came across a paper that discusses motivation theories in the context of engineering education, and, even better, tailored to telling teaching assistants how they can improve their classes: “Motivating Learners: A Primer for Engineering Teaching Assistants” by Torres-Ayala and Herman, 2012. They give a great overview over theories on motivation, and today I want to talk about one of them:

Goal theory

Goal theory describes the different reasons why students engage in academic tasks. There are two different kinds of drivers students can have, avoidance or approach, and two kinds of quality of learning they can be striving for: performance and mastery.

Students who are in a state of avoidance and look for performance will state something like “I don’t want to fail this class!”, whereas students in avoidance striving for mastery will say “I don’t want to look or feel stupid!”. Students with an “approach” attitude, on the other hand, will say “I want to get an A!” if they are aiming at performance, or “I want to understand this material, so I can do … with it”.

Folie3

Illustration of the different kinds of motivation described by the goal theory of motivation

While all four kinds of motivation for learning will produce some kind of learning, students with an approach mindset striving for mastery will be the most intrinsically motivated students who will likely do best.

So what does this mean for your teaching? Making students learn to avoid repercussions or public shaming, hence driving them into an avoidance mindset, is not as effective as creating a learning environment where students work towards something positive. And while having students work to earn, for example, bonus points gets them going in the short run, in the long run it is much more effective to help them discover what they can use the skills and knowledge for in their own lives for, discover the intrinsic value in them, and strive to learn because they want to apply the knowledge and skills to better their own future.

Or, as the authors say: Dangle a carrot to pursue rather than threatening with a whip.

—
Ana T. Torres-Ayala, & Geoffrey L. Herman (2012). Motivating Learners: A Primer for Engineering Teaching Assistants American Society for Engineering Education

Can there be “too much” instruction? Apparently yes!

Leave a reply

I recently, via the blogpost “lessons from a toy” by Eyler (2015), came across the article “The Double-edged Sword of Pedagogy: Instruction limits spontaneous exploration and discovery” by Bonawitz, Shafto, Gweon, Goodman, Spelke and Schulz (2011). The article sets out to find out whether children primarily learn from instruction or from exploration. 85 pre-schoolers are divided into four groups that are exposed to a toy under different conditions.

  • In the pedagogical condition, the experimenter said “Look at my toy! This is my toy. I’m going to show you how my toy works. Watch this!” and then demonstrated one function of the toy. She then exclaimed “Wow, see that? This is how my toy works!” and demonstrated the function again.
  • In the interrupted condition, the experimenter began the same way, but after the first demonstration came up with an excuse and left, without reinforcing the message and demonstrating again.
  • In the naive condition, the experimenter seemed to accidentally discover the function of the toy.
  • In the baseline condition, the experimenter just presented the toy without demonstrating its function.

In all four groups, the experimenter then left the toy with the kid and said “Wow, isn’t that cool? I’m going to let you play and see if you can figure out how this toy works. Let me know when you’re done!”. When the child stopped playing with the toy, the experimenter asked whether the child was done, and only when it answered “yes”, the experiment was concluded.

Analysis of the time each child spent with the toy and of the number of functions a child discovered is fascinating. Children who had been in the pedagogical condition group spent less time with the toy, and didn’t explore nearly as much as the kids in the other groups when left to their devices. Instead, they spent the little time they spent on the toy mainly on the one function that had been demonstrated to them. Children in the baseline group, on the other hand, spent the most time with the toy and discovered the most different functions.

In a second study, the authors place children in situations where they overhear the experimenter explain the toy either to another child or to an adult. They find that when kids overheard the toy being explained to another child, the effect was similar to when the toy was explained to them directly, whereas when the toy was explained to a grown-up, they were more free in their exploration of the toy later on. In their words, “preschool children rationally extend their assumptions about pedagogical situations to contexts in which they overhear instruction to comparable learners”.

To conclude, the authors state that “the current results suggest that instruction leads to inductive biases that create a genuine “double-edged” sword: teaching simultaneously confers advantages for learning instructed information and disadvantages for learning untaught information. Thus, the decision about how to balance direct instruction and discovery learning depends largely on the lesson to be learned.”

And while this study was done on pre-schoolers, I think there is a lot we can learn from it for higher education, too. Yes, of course there is some information that all our students need to learn and for which direct instruction might be the best way forward. But if we want to educate future researchers, then shouldn’t our labs be a lot more about exploration and a lot less about following instructions? Shouldn’t the questions we ask be a lot more open? Shouldn’t there be time for exploration and discovery?

—

Bonawitz, E., Shafto, P., Gweon, H., Goodman, N., Spelke, E., & Schulz, L. (2011). The double-edged sword of pedagogy: Instruction limits spontaneous exploration and discovery Cognition, 120 (3), 322-330 DOI: 10.1016/j.cognition.2010.10.001

When math hurts

Leave a reply

One of the larger projects I am currently working on deals with connecting the math courses, which are compulsory for all freshmen at my university and taught for most students together, with the other subjects they are taking at the same time. Our assumption (which we are testing as we are trying the new setup) is that once students see the relevance of the content of the math courses to the subjects they actually chose (e.g. mechanical engineering), they will learn math more easily and feel less resistance towards the content that they otherwise might perceive as dry and unnecessary for their personal goals. So I have been thinking about math and how math is taught a lot recently, especially because I hated math as a subject throughout university. However, my dislike of the subject itself didn’t keep me from studying and doing a PhD and postdoc on theoretical oceanography and numerical modeling, which relied heavily on the skills and methods I learned in math courses, and where using the math was fun. So what is it that makes math courses so painful?

Actually, a study by Lyons and Beilock (2012) shows that it is not actually math that is painful, it is the anticipation of math. In their paper “When Math Hurts: Math Anxiety Predicts Pain Network Activation in Anticipation of Doing Math“, Lyons and Beilock show that the higher levels of anxiety connected to mathematics a person has, the more the region in the brain that is associated with feelings or pain and terror is activated in anticipation of a math task. In other words: the more afraid someone is of math, the more painful and threatening it is to think of the math homework they still have to do. Which, I would think, explains pretty well why the worse you are at math or even think you are at math (for whatever reason, and don’t tell me it’s related to how intelligent someone is!), the more resistance you will feel to just sit down and work on your problem sets or practice that thing you know you should be practicing. So far, so good.

BUT! The authors don’t stop there. What they then found is that when the participants of their study were working on math problems, the activity in that brain area linked to pain and threat is not related to how math-anxious someone is. So DOING math, in contrast to THINKING ABOUT math, is not more painful for people who don’t like math! And that I find pretty fascinating, and potentially very relevant for math teaching.

Potentially, because I am not quite sure yet what to make of it. I’m not done thinking about this, but what if we tried, for example, practicing math at random times throughout all courses, so nobody would have time to build up fear and everybody got to practice a lot? There are of course arguments against this, like the huge effort it would require from the university as a whole, or, more importantly, all the research that shows that it is beneficial to always link back to prior knowledge of a subject so that new experiences and knowledge can be connected to all that was there on that topic before and placed into context, so one would always have to tell people that they are, in fact, practicing math and not mechanics. But maybe it might still be good to place the math skills needed for a mechanical engineering problem with other ways to solve that problem before eventually connecting it to other math stuff? What do you think?

—

Lyons, I., & Beilock, S. (2012). When Math Hurts: Math Anxiety Predicts Pain Network Activation in Anticipation of Doing Math PLoS ONE, 7 (10) DOI: 10.1371/journal.pone.0048076

Drawing to learn II

Leave a reply

From reading the paper on “Drawing to Learn in Science” in my last blog post, I got browsing the literature and I came across the paper “Drawing to learn: How producing graphical representations enhances scientific thinking” by Fan (2015). There, even more reasons for why we should use drawing in instruction are given.

  • Drawing as a mode to observe the world. If we are asked to draw something, we need to look more closely at the thing we are drawing than if we were just asked to “look” at it. By drawing, for example, individual time steps of the breaking of a wave, will let you understand much more about the physics involved than just mindlessly staring at breaking waves over and over. However, for drawing to be effective as a mode to observe the world, the author points out that the opportunity to reflect upon the drawing needs to be provided, the drawing must be compared against reference knowledge and feedback needs to be given. Especially feedback is crucial, as several studies have shown.
  • Drawing as window into ongoing learning. By observing students draw or looking at finished drawings, we can learn a lot about what students think are important features of the topic of their drawing, and what are not. I have used concept maps to look at the kind of general overview my students had over a the whole field of oceanography, and also to show to them how their view of the field developed over the course of the course, but any drawing can tell you about student misconceptions if you look closely.
  • Drawing to solve problems. When looking at physics problems, if the problem isn’t given in form of a sketch already, the intuitive first step is to draw a sketch and annotate it with the relevant numbers rather than work with a paragraph of text. Drawing in this case is an important skill to solve problems.
  • Drawing to communicate. We have talked about this in the last post, but authors of this paper elaborate on a different very interesting aspect: How drawings follow social norms. The more a group of people draws together, the more similar their drawings become, and the fewer details are necessary to convey the same meaning. This is visible for example when looking at pictograms. The ones that I encounter where I live all make intuitive sense, however when traveling abroad, there are often funny signs where the meaning isn’t at all obvious to visitors…
  • Drawing to explain. The authors give the example of “how a bike pump works” as benefitting from being drawn rather than explained verbally. And as discussed in the last post, drawings are a great basis to convey ideas from.

So once more — drawing is even more important that I thought, and we should definitely provide more drawing opportunities in instruction!

—

Fan, J. (2015). Drawing to learn: How producing graphical representations enhances scientific thinking. Translational Issues in Psychological Science, 1 (2), 170-181 DOI: 10.1037/tps0000037

Drawing to learn

1 Reply

On the sciencegeekgirl blog (which, if you don’t follow it already, you should definitely start now!) there recently was a post on “drawing to learn sketching and peer instruction“. She there discusses the paper “Drawing to Learn in Science” by Ainsworth, Prain, and Tytler (2011). The authors give five reasons why students should draw in science classes:

  1. Drawing to enhance engagement. Drawing gets students engaged in a different way than “just” listening to lectures. Drawing creates emotions towards and involvement with the content you are drawing. Drawing enhances motivation to learn about the topic.
  2. Drawing to learn to represent in science. Drawing your own diagrams or representations means that you learn to better read other people’s diagrams, that you recognize what is important in different types of representations and how they work. I have often asked students to translate temperature and salinity profiles to T-S-diagrams, or vice versa, and seeing how differently the depth-axis is represented, for example, is really powerful.
  3. Drawing to reason in science. Drawing sketches of concepts helps understand them more deeply as now for example directions of forces or characteristic shapes of graphs have to be committed to paper.
  4. Drawing as a learning strategy. Converting a concept from its verbal description to a graphic representation makes it clear very quickly whether or not the concept has been understood or where there are still gaps in understanding.
  5. Drawing to communicate. By drawing, you make your own thoughts visible to the world in a very powerful way, and visualizations help making sure that you and your students or peers are talking about the same thing.

I’m a very visual learner myself, and I always draw everything in order to understand it (see, for example, the header of my blog if you need proof). But somehow I thought that was a learning strategy that everybody uses anyway, so it was really eye-opening to me to read all the reasons why we should use drawing more in instruction to support learning. And there are more reasons for drawing – stay tuned for the next blog post discussing a different paper!

Finally, sciencegeekgirl offers a way to bring the individual drawings back into a large classroom, by suggesting multiple choice questions of typical representations students might come up with, where students pick the one that most closely resembles their own drawing. It is probably not easy to come up with good answer choices the first time you use drawing in your classroom, but if you browse student answers or even collect them, it’ll get so much easier the next year… ;-)

—
Ainsworth, S., Prain, V., & Tytler, R. (2011). Drawing to Learn in Science Science, 333 (6046), 1096-1097 DOI: 10.1126/science.1204153

Of the importance of giving opportunities to practice

Leave a reply
When you are short on time and want to teach as much as possible in a given time, how do you allocate time to different activities and are there any that you might be able to drop? Classically, practice is often pushed into homework assignments or private study time, but a study shows that this might not be a good choice.
There are many elements of instruction that are often combined based on gut-feeling. Martin, Klein and Sullivan (2007) investigate “the impact of instructional elements in computer-based instruction” in a systematic way in order to investigate the impact of several elements of instruction on student learning. The elements of instruction they separate are
  • objectives (statements describing intended learning outcomes that can help students by giving them structures in which to organize new material)
  • information (presentation of the actual content students are supposed to be learning)
  • practice with feedback (the element of instruction where performance is elicited and where learners confirm their correct understanding)
  • examples (examples as well as non-examples, analogies or graphical representations provide additional clarification to learners)
  • review (reinforcing learning at the end of instruction by repeating an outline of the key information)
The authors create 6 groups which contain a comparable mix of students according to a pre-test, and each of the groups is assigned a different e-learning setup. The setups differ such that one contains the full program, one the program without content related to the objectives, one the program without content related to examples, one the program without content related to review, one the program without content related to practice and the final one consisting of information only.
The result is that practice is the one instructional element that has the biggest impact on learner achievement. Students that were assigned the program without practice or the “lean” program did significantly worse on the post test than all other groups. Removal of no other element from the full program had a similar effect.
What do we learn from that study? Granted, it was one study and in computer-based instruction. But I think the message is quite clear: Practice is important. And it is not sufficient to tell students to practice, but opportunities for practice need to be provided. Quite often we think that if we convey the information in a nice way, with a good structure and including examples, that should be sufficient. But this study should make us think twice and drop other elements of instruction before cutting back on practice time.
—

Martin, F., Klein, J., & Sullivan, H. (2007). The impact of instructional elements in computer-based instruction British Journal of Educational Technology, 38 (4), 623-636 DOI: 10.1111/j.1467-8535.2006.00670.x

How do you make sure your students come prepared to your flipped course?

Leave a reply
As I mentioned a while back, we are preparing a flipped course. And the biggest question always is how to make sure students actually prepare for class. Because if they weren’t prepared, what would you do? Repeat the content they should have read about at home and bore the few students who actually did the reading, risking that they won’t bother reading before the next class? Just pretend everybody did their reading even though they clearly don’t have a clue what you are talking about, hoping that they’ll see the necessity of preparing for your next class? Either option isn’t very tempting.
But luckily I came across a study by Heiner, Banet and Wieman (2014): “Preparing students for class: How to get 80% of students reading the textbook before class”. They describe two introductory courses, physics and physiology, where they tested the method they describe, and they find that 80% of students regularly read the textbook (a lot more than what we would expect and than what has previously been reported!). So what is the secret?
They give explicit best practice suggestions, but here is what I took away from the article:
  1. Make sure the pre-read material is actually necessary for the class! So build on it rather than re-teaching it.
  2. Keep the readings short and with a clear connection to the next class. In the study, they pointed out which parts of the texts were essential and which were not.
  3. “Force” the students to look into the textbook. By referring to figures in the textbook rather than reproducing the figures in the online test, students actually have to find the book and open it – a big threshold to reading overcome right here and my favorite trick!
  4. Don’t just prescribe reading, make sure to give opportunity for practice and feedback as well. In the study, they give a 10-15 minute quiz as part of each one-hour assignment.
  5. In your quizzes, make sure the questions are easy to answer for those students who did the pre-reading assignments, and difficult for everybody else.
  6. Explain and remind students of the purpose of the reading: To prepare them for class so class time can be spent more efficiently and the expertise of the instructor is used better.

Another very encouraging finding of the study is that students report benefits of the pre-readings, for example being prepared for class, managing to keep up with the pace of class or getting feedback on their knowledge. 75% of the students state that the pre-readings were helpful for their learning (which is incidentally a higher percentage than those who mention that marks motivated them to do the readings! But since the latter one was in response to an open question this isn’t a fair comparison ;-).

Are you flipping your class already? Any advice for us?

—

Heiner, C., Banet, A., & Wieman, C. (2014). Preparing students for class: How to get 80% of students reading the textbook before class American Journal of Physics, 82 (10), 989-996 DOI: 10.1119/1.4895008

Why care about ocean literacy?

Leave a reply

Ocean literacy, the “understanding of the ocean’s influence on you – and your influence on the ocean”, is obviously a topic near and dear to my heart. But a recent paper by Guest, Lotze and Wallace (2015) on “Youth and the sea: Ocean literacy in Nova Scotia, Canada” makes ocean education seem even more important.

In a study of more than 700 students between the age of 12 and 18 in Nova Scotia, Canada, the authors found that those students who reported greater interaction with the ocean also showed more knowledge about the ocean. The authors also found a significant positive correlation between knowledge about the ocean and the value students placed on the ocean, suggesting that in order to raise awareness of the importance of the ocean, a good first step might be to expose students to the ocean more, and then in a second step provide more ocean education.

Interestingly, the authors find that the students have a lot more knowledge about – and interest in – topics related to ocean life than topics related to ocean physics or chemistry. This is maybe not surprising, and seeing that most ocean issues are “sold” using marine life (“Arctic sea ice melting? Poor polar bears!” or “Ocean acidification? What will that do to Nemo-like clown fish who live on reefs?”) this seems to be a good approach. But ultimately the big issues out there are not exclusively related to marine life. And it’s a bit of a hen-and-egg problem: Are they more interested in marine life because it seems to work as a hook and hence they’ve been exposed to it more, or are they exposed to it more because it does work as a hook and hence they are more interested in it?

To contribute to a society that values and protects our ocean, using the pre-existing interest in any kind of oceanography to get students engaged with the ocean as a much larger system seems like a good plan in any case. The authors suggest using more experiential learning methods to expose students to the ocean, and hence raise their interest and knowledge and ultimately the value they place on the ocean. And that is exactly what I am planning to do, for example at Forscherfreizeit Ratzeburg :-)

For inspiration on what YOU could do, check out the European Marine Science Educators’ Association EMSEA’s facebook page. Always great stuff to be found there!

IMG_8706

Students learning how to do oceanographic measurements

Multiple representations – a better chance to understand what’s going on?

Leave a reply

I’m currently advising a team of teachers who have taken great care to make sure they all use the same representations of a problem. They use the same symbols, have agreed on what kind of diagrams they use, even sketch the problems using the same blue print. They are pretty proud that they have gone to all that trouble to make sure their students don’t get confused. And they got pretty confused themselves when I suggested that they might not be doing their students a favor.

Why would I say that? Well, because evidence suggests it. For example the paper “An Overview of Recent Research on Multiple Representations” by Rosengrant et al., 2007.

The authors compare multiple representations of the same problem (for example text, sketch, motion/free-body/… diagram, graph, computer simulation, mathematical equation). And they find that the more representations students get to know when they learn new content, the easier they learn the content and the easier it is for them to interpret other representations later.

Students who, on an exam, used representations in addition to the mathematical representation that was given to think about a problem, have higher grades. But only if their representations are correct! If students construct incorrect representations (like incorrect free body diagrams), they actually have a lower chance to correctly solve the problem than if they did not draw a representation.
When posing problems, this applies as well. The same student might be able to answer a text-based question, but not an isomorphic question when it is posed as a vector diagram.
Hence, learning multiple representations might be confusing in the very short run, but in the long run students need to learn to deal with them anyway. And representations are important for student learning – if students can construct a different representation of a given problem, they are likely to be able to solve it.
Kind of reminds you of desirable difficulties, doesn’t it?

—

David Rosengrant, Eugenia Etkina, & Alan Van Heuvelen (2007). An Overview of Recent Research on Multiple Representations AIP Conference Proceedings Volume 883 DOI: 10.1063/1.2508714