My dad keeps asking me about a claim I made in my post about the curvature of the Earth: That looking at sea level across a 500 m wide part of a lake, we should be missing the bottom 20 cm of ships moored on the other side. So to shut him up, here are the calculations.
First: This is what we assume:
- The Earth is round.
- Its radius is 6.371 km.
- We can actually see in a straight line and the light isn’t bent by weird things in the air or other processes.
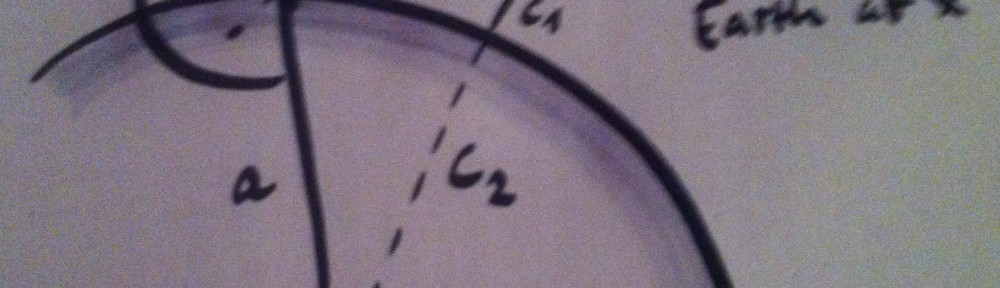
This gives us this situation:
We are situated at position x right at water level. We look out tangentially along b, so there is a right angle between the radius of the Earth, a, and b. Side c of the triangle we are looking at consists of c2 (which is equal to a, the radius of the Earth) and c1, which we are looking for: The height below which we cannot see from position x.
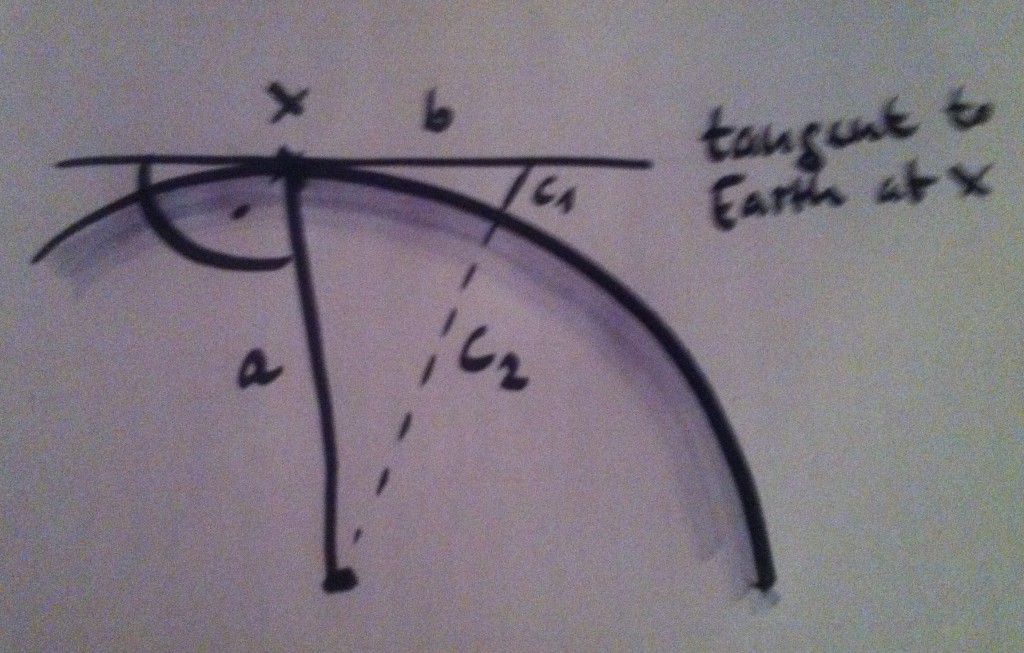
Calculating how much we cannot see at a given distance looking at water level.
We know a to be 6,371 km and b is 0.5 km. Now we just need to put everything into Pythagoras’ theorem, solve for c1 and we are done!
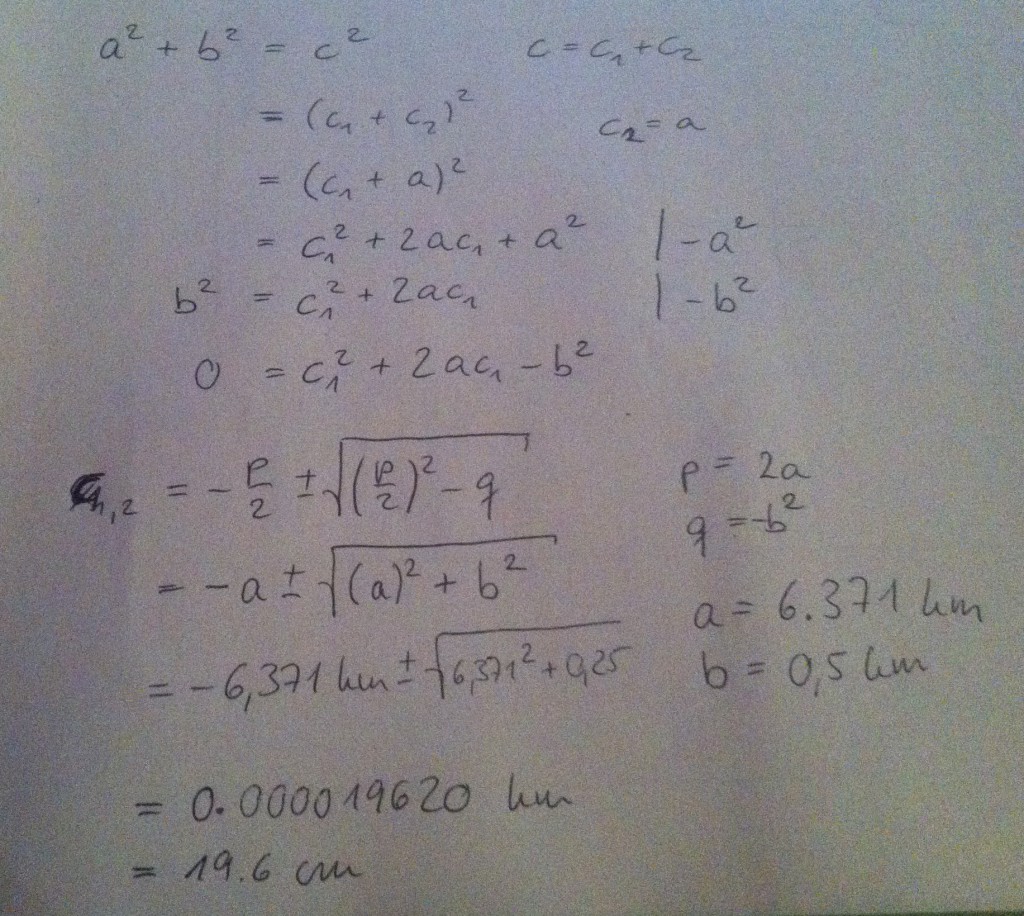
Calculating how much we cannot see at a given distance looking at water level. Are you sure you really want to look at this?
Turns out we find c1 as 19.6 cm. Which is pretty close to the 20 cm I claimed last time, right? Everybody happy now? If you want to look at a more realistic and less simplified calculation – go do it yourself! :-)