![[photo] Picture of Mirjam smiling in the camera to show how happy it would make me if this showed up on Twitter](https://mirjamglessmer.com/wp-content/uploads/2020/11/IMG_0168-624x468.jpg)
Category Archives: Uncategorized
![[photo] Picture of Mirjam smiling in the camera to show how happy it would make me if this showed up on Twitter](https://mirjamglessmer.com/wp-content/uploads/2020/11/IMG_0168-624x468.jpg)
![[photo] Picture of Mirjam smiling in the camera to show how happy it would make me if this showed up on Twitter](https://mirjamglessmer.com/wp-content/uploads/2020/11/IMG_0168-624x468.jpg)
Exciting life update! Joining GFI as adj assoc prof! :-)
It’s been in the making for a while, but I am super excited to announce that I will be joining the Geophysical Institute at the University of Bergen as an adjunct associate professor!
Here is a video I filmed to introduce myself at the institute’s meeting today that I sadly couldn’t attend.
I am very excited to be working more closely with many super awesome colleagues — Elin, Kjersti, Tor to just name a few — and to have an excuse to be in Bergen more often!
If you want to celebrate with me, there are several options:
Option 1: Do some #KitchenOceanograpy!
From next Tuesday onwards, there will be a new kitchen oceanography experiment each and every day for 24 days (also in German and in Norwegian)! Follow along, take pictures, post them on social media, tag me and let’s talk about some exciting ocean physics!

Option 2: Go #WaveWatching and send me a #FriendlyWaves!
You know the drill: Enjoy some wave watching, take a pic, post it on social media, tag me, and let’s talk about what physics are behind the waves you saw! And about how awesome oceanography and water are ;-)

Pop-up beach walk
Strong west winds aren’t the best for traditional wave watching on the east coast, but we got beaches in places where we usually don’t have them! Pretty exciting, especially since I’m on a home office day (luckily the trains to work don’t run regularly because of the storm, so I got to squeeze in some beach time before work!).
Below, you see where the big storm drain runs into Kiel fjord. You might remember it, because it’s the one that the fluorescent dye tracer comes out of whenever the city’s heating systems leak. Except that usually there is a lot more water around here…

So this is a pretty unusual perspective!

Also walking underneath these bridges is usually not recommended.

But it’s pretty cool to see these familiar structures from a very different perspective!

Something I found super interesting about this picture is this little groove that has formed underneath the edge of the bridge. What it shows us is that it has rained a lot at a time when the water was already gone, because that’s how this groove got formed! if there was still water around when the rain ran off the bridge, a) any “impact” of drops would have been dampened a lot by hitting water and b) waves would have acted to remove the groove and shape the sea floor in whatever other way they liked. So fun to discover these things! A bit like playing detective :-D

Maybe rubber boots would have been more appropriate…

Definitely interesting perspectives from down here!

But: Breaking waves on the beach! That’s not something we see a lot around here!

And finally a better look at the obstacle these stilts are there to keep boats off of.

It’s definitely a very different experience to my usual walks along here!

And even some rock pooling today!

#DryTheory2JuicyReality featured in our university’s newspaper!
We’ve had a busy couple of weeks at #DryTheory2JuicyReality with our new rotating table, our seminar presentation last week, attending BOOT in Düsseldorf, and more, all in the name of science communication.
Super nice to see our efforts recognized in print: Our project was featured in the university newspaper! Read about us here in German and in English!

Happy #CTDAppreciationDay!
For #CTDAppreciationDay, I am re-sharing a video that Sindre Skrede (find him on twitter or vimeo for many more exciting pictures and movies!) and I made in 2011 (!!).
I am still super proud of this work because I first narrated it in Norwegian (after only having lived in Norway for a couple of months and having started classes only after moving there! Scary stuff, but I did it!), and we only translated it to English afterwards. Also I think we did a great job there!

Burning soap bubbles
The other day I was thinking about fun experiments to do on a Birthday party for kids (won’t spoiler here whose kid that might be, and also, coincidentally, it was on Jenny’s Birthday! Happy Birthday, Jenny! :-)) and I realized I never posted the “burning soap bubbles”. Probably because I still can’t think of a good reason why it belongs on a blog on “adventures in teaching and oceanography”, but since I dug out the movies that my friend Dési made and narrated more than 2 years ago, and it’s fun to watch, (and also it’s much faster for me to google my blog for this experiment than to search for it on my phone if I ever need it again): here we go!
English short version of Dési’s narration: Take dish soap and mix it in water. Bubble lighter gas into the water to create bubbles. Take them up in your hand, bring a lighter close, and that’s it! It doesn’t get hot or anything, but it looks very impressive!

Networking event for online science communicators tomorrow!
Anticipation is rising, just one more sleep and then it’s finally here! The networking event for online science communicators that Alice (see her blog, twitter, Instagram — see, we are serious about online science communication!) and I are organizing here in Kiel!
Check it out here and make sure to register if you want to join us, the address given on the website is unfortunately not where we’ll be!


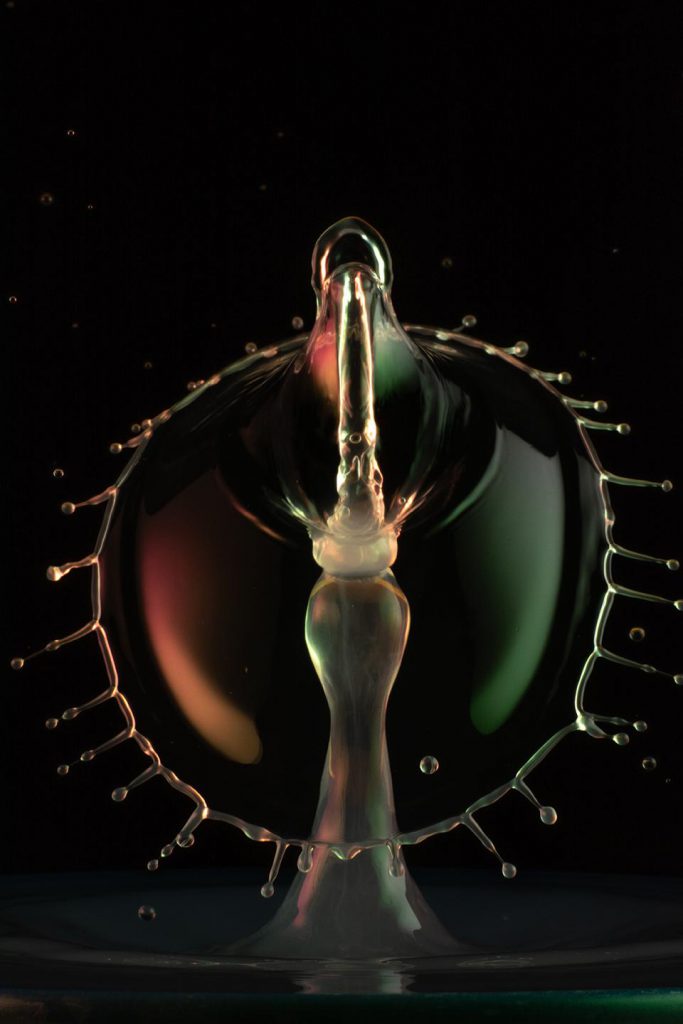
#DropPhotography. Art or physics? Art AND physics!
When I take pictures of drops, they look like the picture below (which I showed in a blogpost yesterday), but I see tons of physics everywhere. Ring-shaped waves! Drops jumping up due to surface tension! Interference pattern of overlapping waves! And much more.

When Wlodek Brühl takes pictures of drops, they look like below. As an artist, to him it’s all about composition and inspiration and expression.
And when we work together, lots of interesting things happen. Do you want to see our art and science collaboration in action? Then come join one of our workshops at Digitale Woche Kiel, both on September 8th, 2019, one at 11-13 and the other at 13:30-15:30. Could you think of anything more inspiring to do on a Sunday? :-)

Favourite quote by Miriam Goldstein: “The ocean is strong and powerful and it likes to rip things up”
I am so lazy (or so efficient?) that even my doodles are multi purpose. Like this one, which is one of my three favourite ocean-related quotes I promised to illustrate to celebrate my blog’s 6th Birthday, and it’s also my submission to September’s #scicommchall on drawing the inspiration to your work.
Kim suggested I should draw Miriam Goldstein‘s “The ocean is strong and powerful and it likes to rip things up”, which I just love. For scientific context of this quote, check out Clark Richard’s blog post on Deep Sea News — a brilliant article on the (ocean) physics of the Ocean Cleanups System.


New favourite ocean quote: You are not a drop in the ocean, you are the ocean in a drop
As part of my blog’s 6th Birthday celebration, I asked you to submit your favourite ocean quotes so I could illustrate them for you. This is what Benjamin suggested (and I love it!).

P.S.: The quote might be by Rumi, but in total, my internet research was inconclusive as to the original source. Since I had already taken the pictures of my drawing anyway, we’ll have to live with a non-attributed quote…
