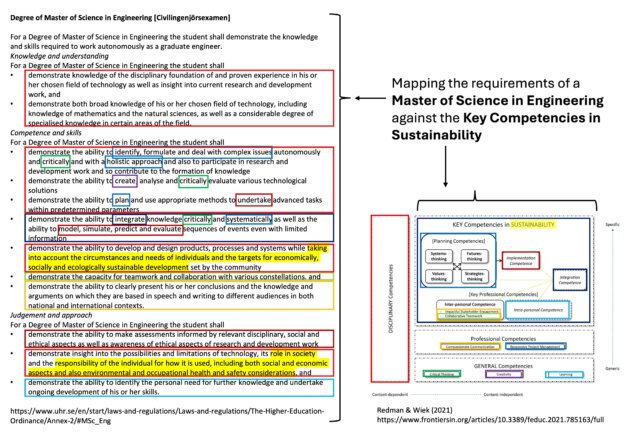
Students can engage in higher education in different ways: behavioral, emotional, cognitive, or in any combination of those. Traditionally, this is seen as engagement with the curriculum inside the classroom, but increasingly the view of student engagement is widened to include forms where students take more ownership of their own learning, for example when becoming involved in (re)designing curriculum as student partners who are currently taking a course (or not), co-creating learning with a whole course, influencing learning on a program level (whether enrolled in the program or not), or influencing the bigger setting through engagement with services like university libraries, or in developing religious diversity training. In the book “Advancing Student Engagement in Higher Education: Reflection, Critique and Challenge”, Lowe (2023) brings together 25 chapters from 36 contributors, exploring and highlighting different aspects from very different perspectives. I am summarizing my personal main takeaways below.
Continue reading →